Une série temporelle est une suite d’observations ordonnées dans le temps : \({X_t}, t \in \mathbb{T}\) où :
- \(t\) représente le temps (jours, mois, années, instants discrets)
- \(X_t\) est la valeur observée au temps t
L’analyse des séries temporelles permet de :
- Décrire l’évolution d’un phénomène dans le temps
- Comprendre sa structure (tendance, saisonnalité, cycles)
- Prévoir les valeurs futures
- Détecter des anomalies ou ruptures
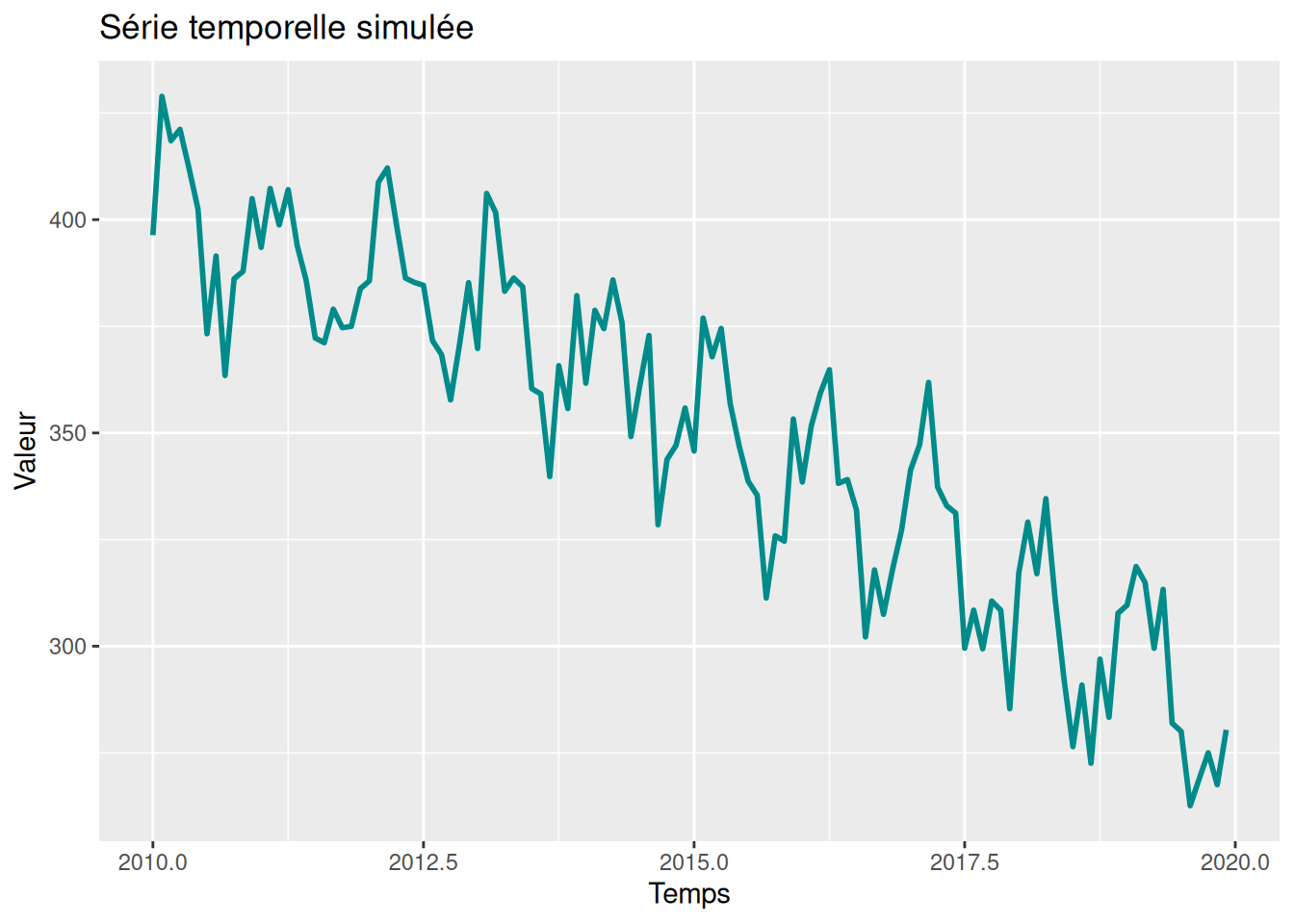
Première simulation
Générons une séries comme la somme de trois composantes \(X_t = m_t + s_t + Z_t\) où :
- \(m_t\) est la tendance (évolution de long terme)
- \(s_t\) est la composante saisonnière (effet périodique)
- \(Z_t\) est un bruit aléatoire (composante irrégulière)
Code
n <- 120 # Nombre d observations
p <- 12 # periode
t <- seq(1,n) # temps
m_t <- 400 - 0.5 * t - 1/ (2*n) * t^2 # tendance polynomiale deterministe
s_t <- 20 * sin(2 * pi * t / p) # tendance saisonniere p-periodique
Z_t <- rnorm(n, 0, 10) # bruit
X_t <- ts(m_t + s_t + Z_t,
start = c(2010,01),
end = c(2019,12),
frequency = p)
Affichage de la série :
Code
library(ggplot2)
df <- data.frame(
time = as.numeric(time(X_t)),
X_t = as.numeric(X_t),
trend = m_t,
seasonality = s_t,
noise = Z_t
)
ggplot(df, aes(x = time, y = X_t)) +
geom_line(color = "darkcyan", linewidth = 1) +
labs(
title = "Série temporelle simulée",
x = "Temps",
y = "Valeur")
Quelques infos sur la série
start(X_t)
end(X_t)
time(X_t)
frequency(X_t)
# Extraire une fenêtre de la série
window(X_t, start= c(2012,01), end=c(2014,12))
Opérateurs et Filtres
Opérateurs
Les opérateurs temporels sont des transformations appliquées à une série temporelle \(X_t\) qui permettent de manipuler le temps :
- retarder
- avancer
- différencier ou combiner des observations successives
L’opérateur de retard d’ordre k, noté \(B^k\), défini par \(B^k X_t = X_{t-k}\), décale la série de k périodes vers le passé.
L’opérateur d’avance d’ordre k, défini par \(B^{-k} X_t = X_{t+k}\), décale la série vers le futur.
# Opérateur Backward
lag(X_t, 3)
# Opérateur Forward
lag(X_t, -2)
Filtres
Le Filtre de différenciation d’ordre p permet d’éliminer une tendance polynomiale :
\[\Delta^p X_t = (1 - B)^p X_t\]
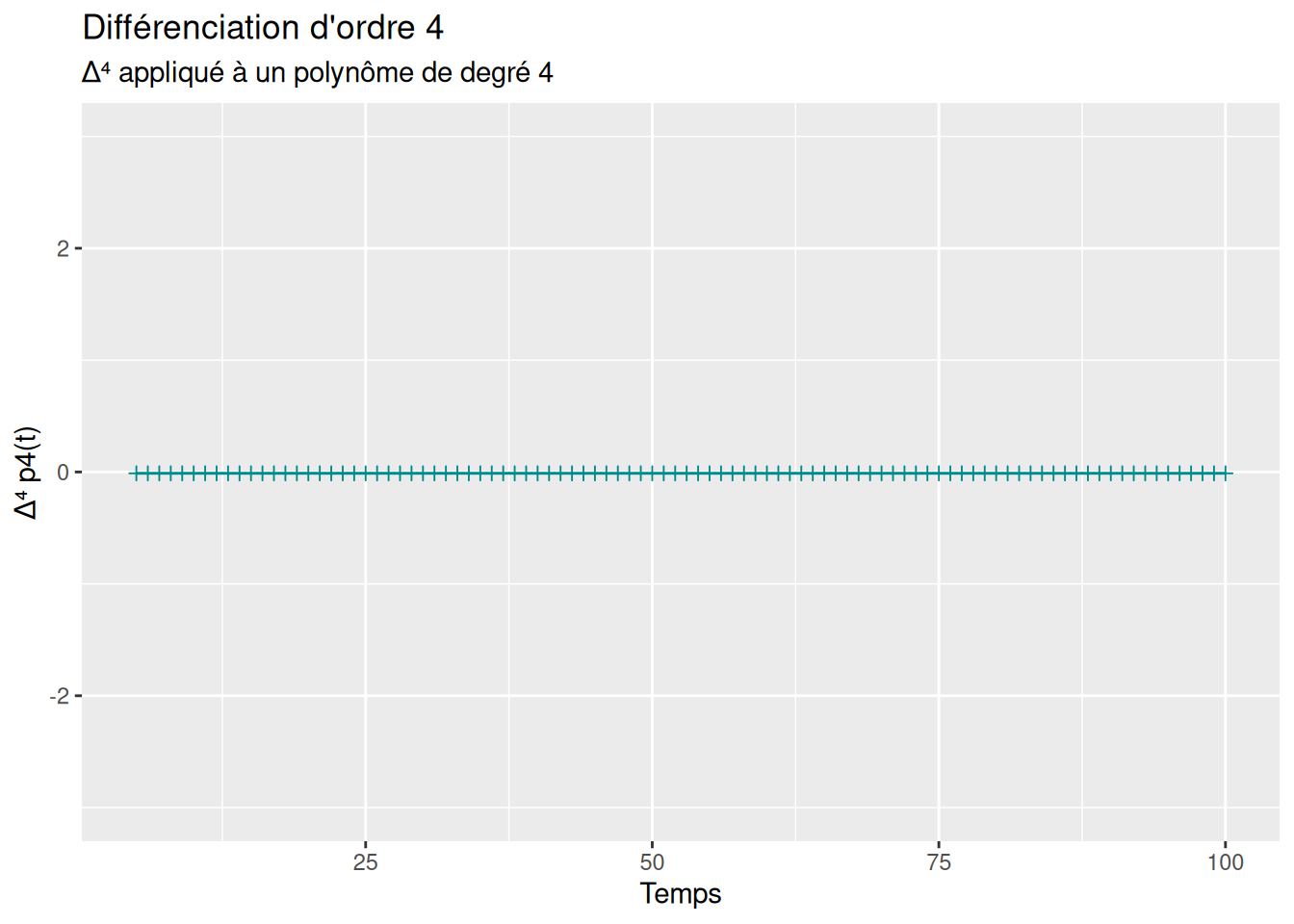
Il transforme les tendances polynomiales en constantes.
\(\Delta^1\) élimine les tendances linéaires, \(\Delta^2\) élimine les tendances quadratiques…
Considèrons un polynôme déterministe de degré 4 :
\[X_t = 10 + \frac{1}{2}t - \frac{1}{10}t^2 + \frac{1}{500}t^3 - \frac{1}{2000}t^4\]
Code
library(ggplot2)
# Temps
n <- 100
t <- seq(1,n)
# Polynôme de degré 4
p4 <- 10 + 0.5 * t - 0.1 * t^2 + 1/500 * t^3 - 1/2000 * t^4
df <- data.frame(t = t, p4 = p4)
Code
df_d1 <- data.frame(
t = t[-1],
diff = diff(p4, differences = 1))
ggplot(df_d1, aes(x = t, y = diff)) +
geom_point(color = "darkcyan", shape = 3) +
geom_line(color = "darkcyan") +
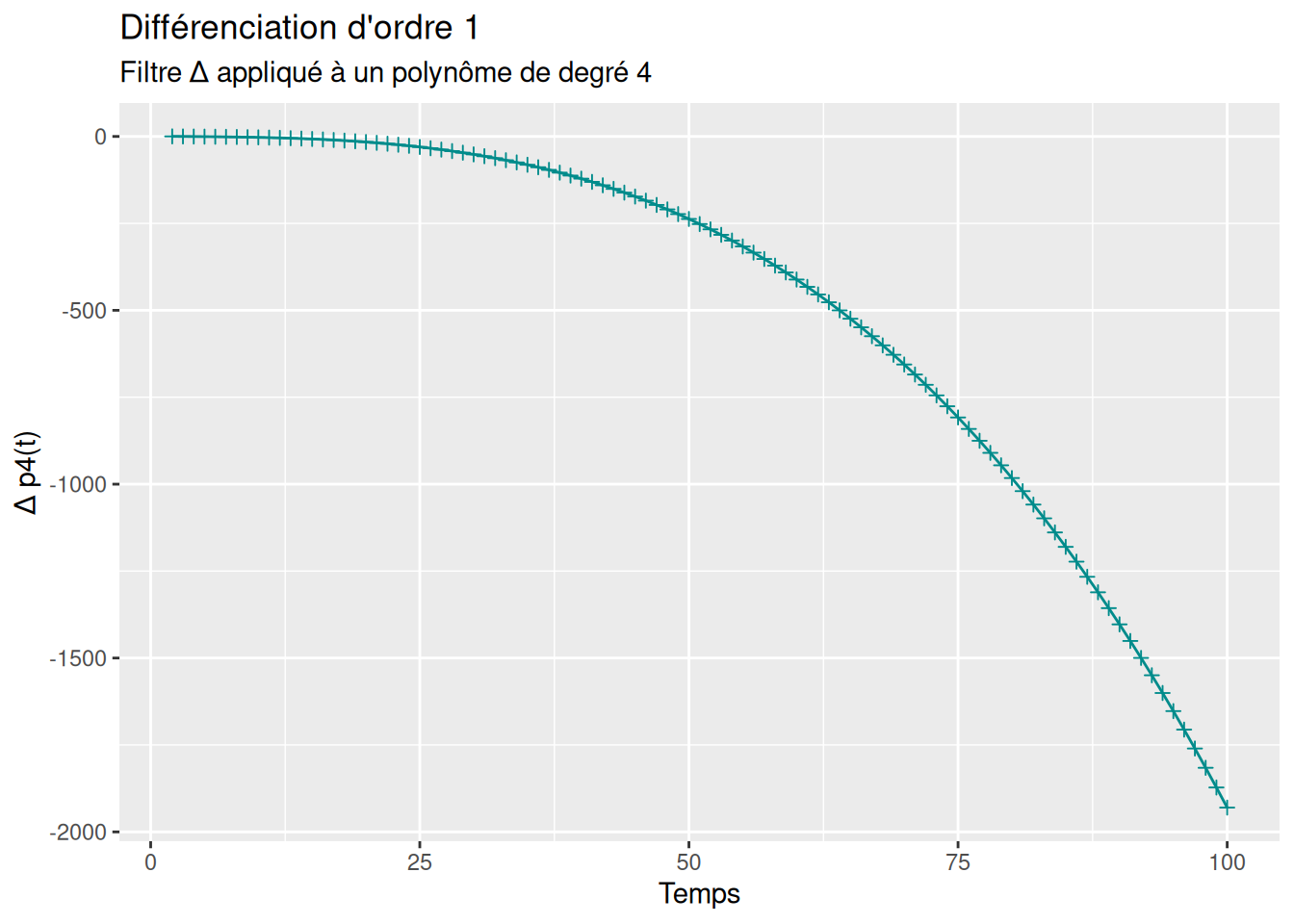
labs(title = "Différenciation d'ordre 1",
subtitle = "Filtre Δ appliqué à un polynôme de degré 4",
x = "Temps",
y = "Δ p4(t)")
Code
df_d2 <- data.frame(
t = t[-c(1,2)],
diff = diff(p4, differences = 2))
ggplot(df_d2, aes(x = t, y = diff)) +
geom_point(color = "darkcyan", shape = 3) +
geom_line(color = "darkcyan") +
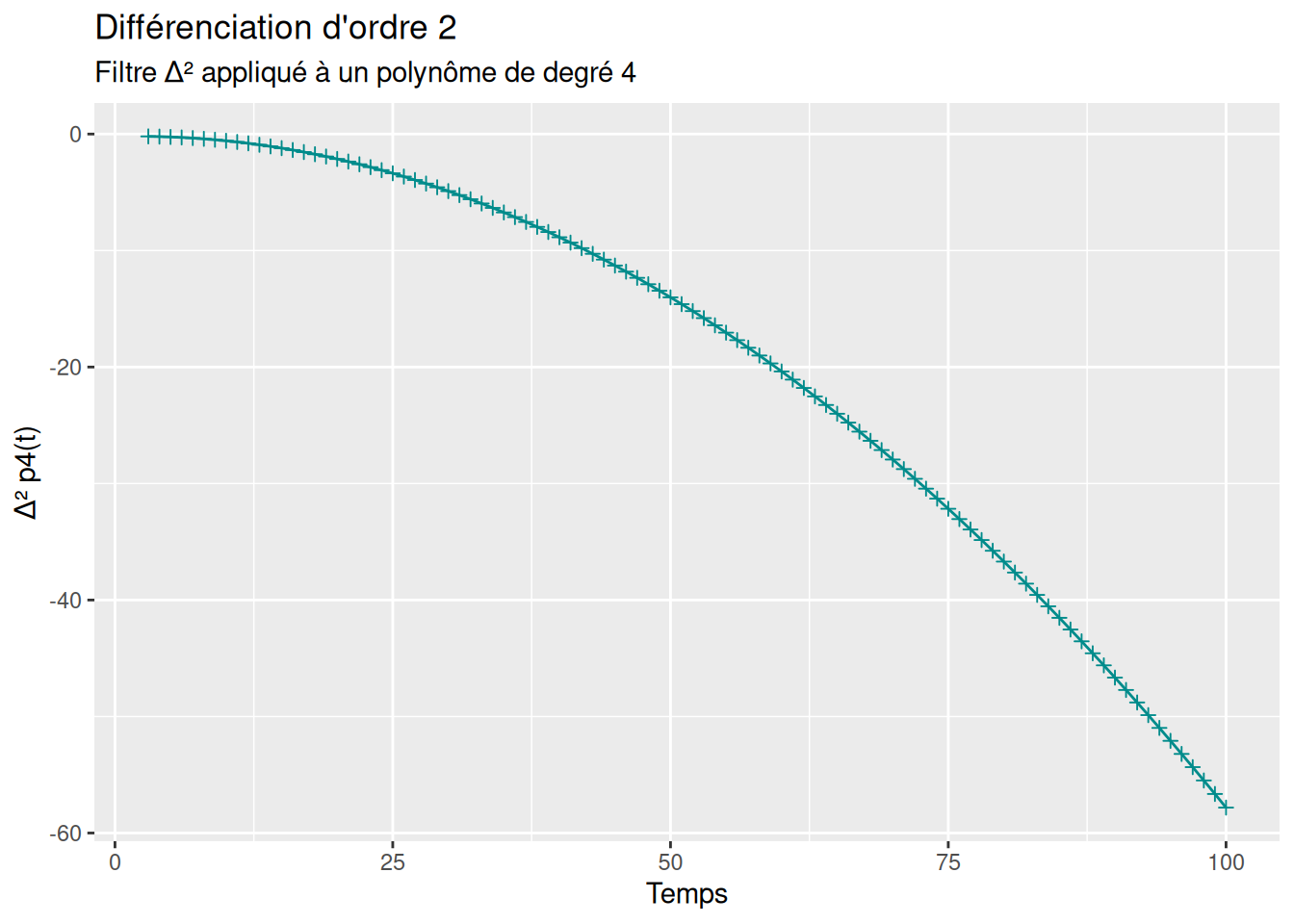
labs(title = "Différenciation d'ordre 2",
subtitle = "Filtre Δ² appliqué à un polynôme de degré 4",
x = "Temps",
y = "Δ² p4(t)")
Code
df_d3 <- data.frame(
t = t[-c(1,2,3)],
diff = diff(p4, differences = 3))
ggplot(df_d3, aes(x = t, y = diff)) +
geom_point(color = "darkcyan", shape = 3) +
geom_line(color = "darkcyan") +
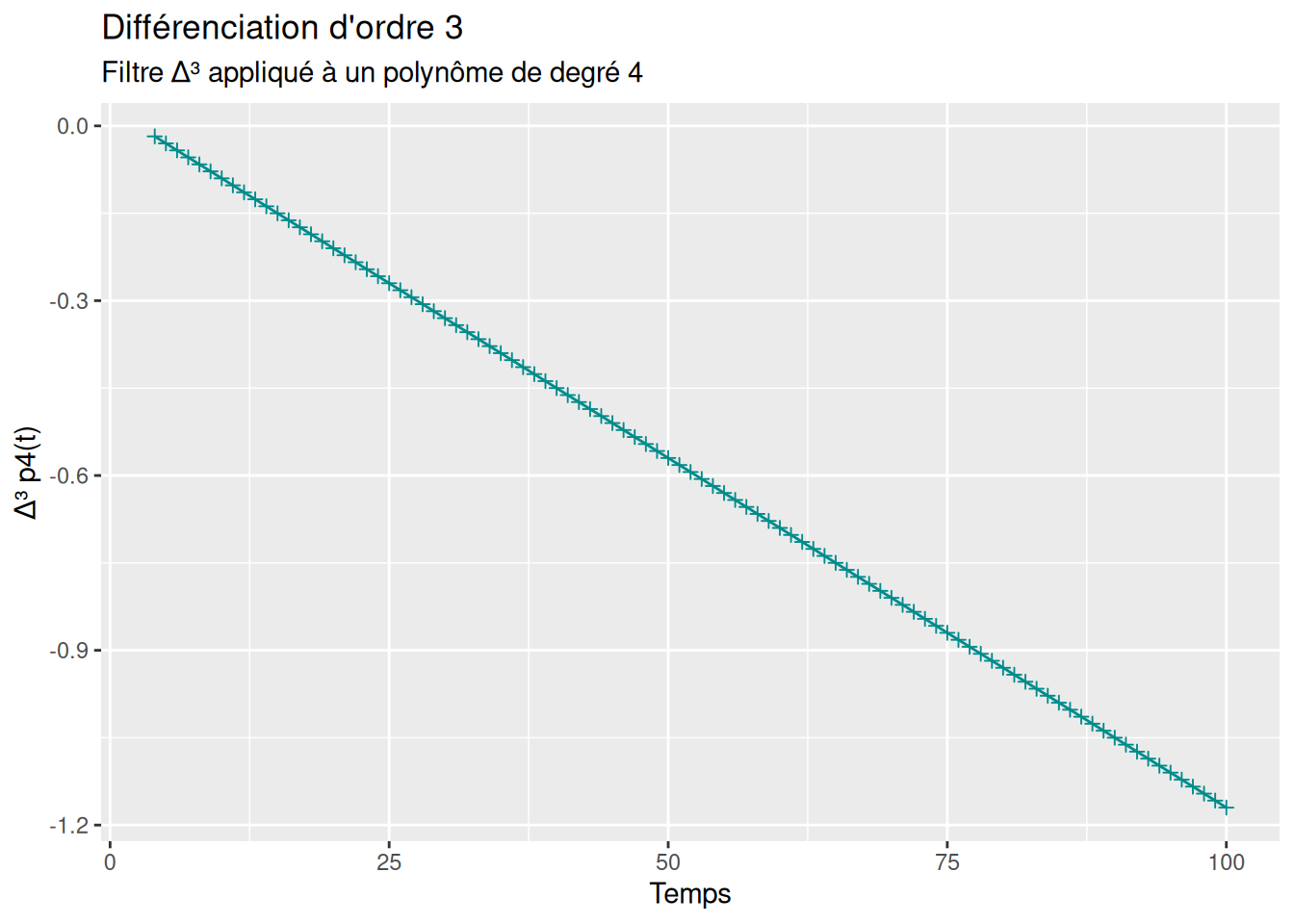
labs(title = "Différenciation d'ordre 3",
subtitle = "Filtre Δ³ appliqué à un polynôme de degré 4",
x = "Temps",
y = "Δ³ p4(t)")
Code
df_d4 <- data.frame(
t = t[-c(1,2,3,4)],
diff = diff(p4, differences = 4)
)
ggplot(df_d4, aes(x = t, y = diff)) +
geom_point(color = "darkcyan", shape = 3) +
geom_line(color = "darkcyan") +
scale_y_continuous(limits = c(-3, 3)) +
labs(title = "Différenciation d'ordre 4",
subtitle = "Δ⁴ appliqué à un polynôme de degré 4",
x = "Temps",
y = "Δ⁴ p4(t)")
Les moyennes mobiles sont des filtres linéaires utilisés pour lisser une série temporelle et éliminer la saisonnalité.
La moyenne mobile arithmétique d’ordre (m) est définie par :
\[\widehat{X}_t = \frac{1}{m} \sum_{k=0}^{m-1} X_{t-k}\]
Une moyenne mobile d’ordre p permet déliminer une saisonnalité de période p.
Moyenne mobile impaire
Si p est impair, la moyenne mobile est centrée naturellement :
\[\widehat{m}_t = \frac{1}{p} \sum_{k=-(p-1)/2}^{(p-1)/2} X_{t+k}\]
Moyenne mobile paire
Si p est pair, le filtre n’est pas centré.
On utilise alors une moyenne mobile doublement centrée :
\[\widehat{m}_t = \frac{1}{p} \left(\frac{1}{2}X_{t-p/2} + \sum_{k=1}^{p-1} X_{t-p/2+k} + \frac{1}{2}X_{t+p/2}\right)\]
Décomposition des séries temporelles
La modélisation
processus AR, MA, ARMA, ARIMA