rm(list=ls())Régression linéaire
🚧
Avant de commencer
Réinitialisation de l’environnement
Librairies utiles
library(dplyr)
library(ggplot2)1 Objectif
Une régression linéaire est une méthode statistique utilisée pour modéliser la relation entre :
- une variable à expliquer notée \(Y\)
- une ou plusieurs variables explicatives linéairement indépendantes (régresseurs), notées \(X_i\)
Notons \(p\) le nombre de regresseurs.
Définir un modèle pour déterminer le prix d’une maison avec 3 régresseurs :
- \(Y\) : Prix
- \(X_1\) : Surface
- \(X_2\) : Nombre de toilettes
- \(X_3\) : Année de construction
Nous disposons d’un échantillon de taille \(n\) pour construire notre modèle :
| Y | X1 | X2 | X3 |
|---|---|---|---|
| 250 000 | 100 | 1 | 1990 |
| 350 000 | 150 | 2 | 2000 |
| 400 000 | 180 | 3 | 2010 |
| 300 000 | 120 | 2 | 1985 |
| 280 000 | 110 | 2 | 2005 |
À partir de ces données, nous souhaitons trouver une fonction \(f\) telle que : \(Y = f(X) + \epsilon\).
Dans le cadre de la régression linéaire, la fonction \(f\) s’exprime simplement : \(f(X) = X\beta\)
Notre modèle devient alors : \(Y = X\beta + \epsilon\) avec :
- \(\beta\) : le coefficient de régression (pente de la droite)
- \(\epsilon\) : le terme d’erreur
\(\epsilon\) est le terme d’erreur (ou résidu). Il représente tout ce qui n’est pas expliqué par \(X\).
En d’autres termes, il capture la différence entre la valeur observée de \(Y\) et la valeur prédite par le modèle.
Le terme \(E\) reflète les variations imprévisibles ou dues à d’autres facteurs non inclus dans le modèle.
Nous considérerons le modèle gaussien, ainsi \(\epsilon ∼ N (0, \sigma^2 Id)\).
L’écriture matricielle du modèle :
\[\begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{pmatrix} = \begin{pmatrix} 1 & x_{11} & x_{12} & x_{13} \\ 1 & x_{21} & x_{22} & x_{23} \\ 1 & x_{31} & x_{32} & x_{33} \\ 1 & x_{41} & x_{42} & x_{43} \\ 1 & x_{51} & x_{52} & x_{53} \end{pmatrix} \begin{pmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \beta_3 \end{pmatrix} + \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \end{pmatrix}\]
Ce qui équivaut à \(\forall i = 1,...,n, Y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i3} + \beta_4 x_{i4}\)
- La première colonne de \(X\) est une colonnes de 1 pour l’intercept
- La seconde colonne de \(X\) est \(X_1\), la 3e est \(X_2\), la 4e est \(X_3\)
L’étape suivante est d’estimer les coefficients du modèle. En utilisant la méthode des moindres carrés ordinaires (MCO), nous recherchons les valeurs des coefficients \(\beta\) qui minimisent la somme des carrés des résidus.
L’estimateur MCO des coefficients \(\beta\) est donné par : \(\hat{\beta} = (X^T X)^{-1} X^T Y\) sous les hypothèses suivantes sur le terme d’erreur :
- \(\mathbb{E}(\epsilon_i) = 0 \ \forall i = 1,...,n\) (centré)
- \(\mathbb{V}(\epsilon_i^2) = \sigma^2 \ \forall i = 1,...,n\) (homoscédastique)
- \(Cov(\epsilon_i, \epsilon_j) = 0, \ 1 \le i \ne j \le n\) (décorrélé)
2 Premier exemple
n <- 200 # Taille de l echantillon
p <- 3 # Nombre de regresseurs2.1 Générerons des données
set.seed(234)
X1 <- runif(n, min=0, max=1)
X2 <- seq(1,n)
X3 <- X1^2 + 1
E <- rnorm(n, mean=0, sd=1)
Y <- 15 + 3*X1 + X2/10 + X3/2 + E
df <- data.frame(X1, X2, X3, Y)
head(df, 10)| X1 | X2 | X3 | Y |
|---|---|---|---|
| 0.7456200 | 1 | 1.555949 | 18.30523 |
| 0.7817124 | 2 | 1.611074 | 19.07200 |
| 0.0200371 | 3 | 1.000401 | 14.91214 |
| 0.7760854 | 4 | 1.602308 | 18.87371 |
| 0.0669101 | 5 | 1.004477 | 13.75483 |
| 0.6447951 | 6 | 1.415761 | 17.99670 |
| 0.9293860 | 7 | 1.863758 | 19.79870 |
| 0.7176422 | 8 | 1.515010 | 17.32157 |
| 0.9277365 | 9 | 1.860695 | 18.84897 |
| 0.2842301 | 10 | 1.080787 | 17.58318 |
2.2 Régression linéaire
Effectuons la régression linéaire de \(Y\) sur \(X_1\), \(X_2\) et \(X_3\) grâce à la fonction lm() (linear model).
Elle va estimer les coefficients \(\beta_0\), \(\beta_1\), \(\beta_2\) et \(\beta_3\) ainsi que la qualité de l’estimation.
reg <- lm(Y ~ X1 + X2 + X3,
data = df)
summary(reg)
Call:
lm(formula = Y ~ X1 + X2 + X3, data = df)
Residuals:
Min 1Q Median 3Q Max
-2.57715 -0.56368 0.04049 0.57072 2.87147
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.801475 0.863889 18.291 < 2e-16 ***
X1 4.840852 1.065220 4.544 9.62e-06 ***
X2 0.102229 0.001189 85.998 < 2e-16 ***
X3 -0.994179 1.035373 -0.960 0.338
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9666 on 196 degrees of freedom
Multiple R-squared: 0.9749, Adjusted R-squared: 0.9745
F-statistic: 2536 on 3 and 196 DF, p-value: < 2.2e-16La fonction summary() fournit le tableau des coefficients avec :
Estimate: les valeurs estimées des coefficients \(\beta\)Std. Error: l’erreur standard associée à chaque coefficient- cela donne une idée de la précision des estimations
t value: test de Student (\(H_0\) : le coefficient est égal à zéro, i.e. la variable explicative n’a pas d’effet sur \(Y\))Pr(>|t|): La p-valeur associée au test- une p-valeur faible indique que le coefficient est statistiquement significatif
***: plus il y a d’étoiles plus le coefficient est significatif
La fonction summary() fournit également des statistiques globales du modèle.
Residual standard error:- l’écart-type des résidus
- mesure la variabilité des valeurs de Y non expliquées par le modèle
Multiple R-squared: R² (Coefficient de détermination)- indique la proportion de la variance de Y expliquée par le modèle
- il varie entre 0 et 1, où 1 indique un ajustement parfait.
F-statistic: test de Fischer de significativité du modèle.- \(H_0\) : tous les coefficients de régression sont égaux à zéro (i.e. les variables explicatives n’ont aucun effet sur \(Y\))
2.3 Application du modèle
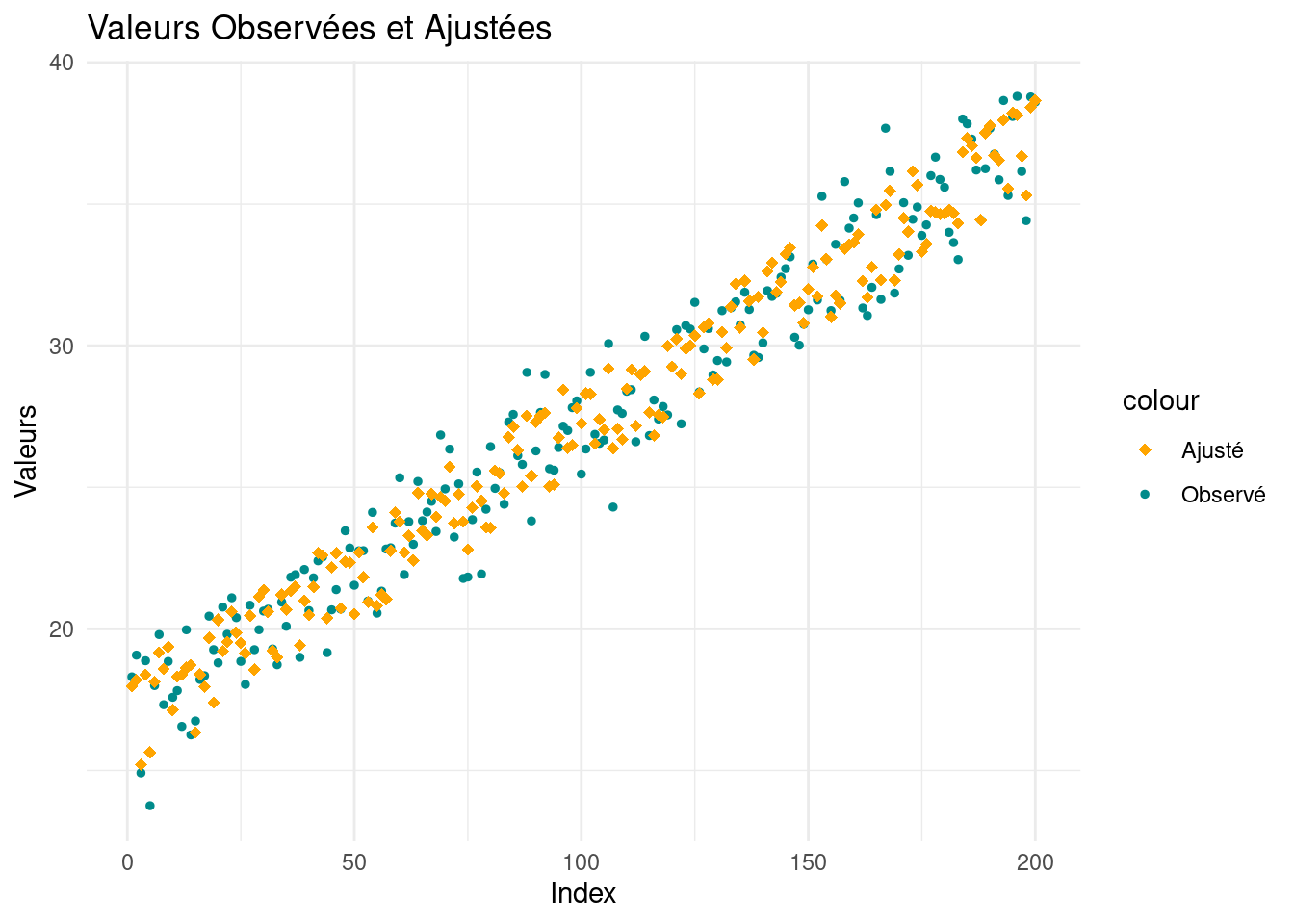
Maintenant que nous avons notre modèle, calculons et affichons :
- les valeurs ajustées \(\hat{Y}\) (prédites par le modèle)
- les résidus \(\hat{\epsilon}\) (différence en la valeur réelle et la valeur prédite)
df$Y_hat <- reg$fitted.values # ou df$Y_hat <- predict(reg, subset(df, select = -c(Y)))
df$Epsilon_hat <- reg$residuals # ou df$Epsilon_hat <- resid(reg) ou df$Epsilon_hat = df$Y - df$Y_hat
head(df, 10)| X1 | X2 | X3 | Y | Y_hat | Epsilon_hat |
|---|---|---|---|---|---|
| 0.7456200 | 1 | 1.555949 | 18.30523 | 17.96625 | 0.3389790 |
| 0.7817124 | 2 | 1.611074 | 19.07200 | 18.18839 | 0.8836105 |
| 0.0200371 | 3 | 1.000401 | 14.91214 | 15.21058 | -0.2984365 |
| 0.7760854 | 4 | 1.602308 | 18.87371 | 18.37432 | 0.4993826 |
| 0.0669101 | 5 | 1.004477 | 13.75483 | 15.63789 | -1.8830648 |
| 0.6447951 | 6 | 1.415761 | 17.99670 | 18.12869 | -0.1319815 |
| 0.9293860 | 7 | 1.863758 | 19.79870 | 19.16319 | 0.6355146 |
| 0.7176422 | 8 | 1.515010 | 17.32157 | 18.58711 | -1.2655409 |
| 0.9277365 | 9 | 1.860695 | 18.84897 | 19.36271 | -0.5137369 |
| 0.2842301 | 10 | 1.080787 | 17.58318 | 17.12518 | 0.4579915 |
ggplot(df, aes(x = 1:nrow(df))) +
geom_point(aes(y = Y, color = "Observé"), size = 1) +
geom_point(aes(y = Y_hat, color = "Ajusté"), shape = 18, size = 2) +
labs(x = "Index", y = "Valeurs", title = "Valeurs Observées et Ajustées") +
scale_color_manual(values = c("Observé" = "darkcyan", "Ajusté" = "orange")) +
theme_minimal()