Probabilité

Concepts basiques de probabilité

1 Formules de base

\[\mathbb{P}(X \leq x) = \mathbb{E}(\mathbb{1}_{X \leq x})\] \[\mathbb{V}(X) = \mathbb{E}((X-\mathbb{E}(X))^2)\]

2 Convergences

• Convergence presque surement
  • \(X_n \underset{n \to +\infty}{\overset{p.s} \longrightarrow} X \Longleftrightarrow \forall \omega \in \Omega, \lim\limits_{n \rightarrow +\infty} X_n(\omega) = X(\omega)\)
• Convergence en probabilité
  • \(X_n \underset{n \to +\infty}{\overset{\mathbb{P}} \longrightarrow} X \Longleftrightarrow \forall \epsilon, \lim\limits_{n \rightarrow +\infty} \mathbb{P}(||X_n-X||>\epsilon) = 0\)
• Convergence dans \(\mathbb{L}^p\)
  • \(X_n \underset{n \to +\infty}{\overset{\mathbb{L}^p} \longrightarrow} X \Longleftrightarrow \lim\limits_{n \rightarrow +\infty} ||X_n-X||_p = 0\)
• Convergence en Loi
  • \(X_n \underset{n \to +\infty}{\overset{\mathcal{L}} \longrightarrow} X \Longleftrightarrow \lim\limits_{n \rightarrow +\infty} \mathbb{E}(h(X_n)) = \mathbb{E}(h(X)), \forall h\) continue bornée

Implications de convergences :

• \(p.s \Rightarrow \mathbb{P}\)
• \(\mathbb{L}^p \Rightarrow \mathbb{P}\)
• \(\mathbb{P} \Rightarrow \mathcal{L}\)

3 Loi forte des Grands Nombres

3.1 Énoncé

Soit \((X_n)_{n\geq1}\) une suite de variables aléatoires indépendantes et identiquement distribuées (iid) et intégrables à valeurs dans \(\mathbb{R}^d\). Alors :

\[\frac{1}{n} \sum_{i=1}^{n} X_i \underset{n \to +\infty}{\overset{\text{p.s.}}{\longrightarrow}} \mathbb{E}(X_1)\]

Formulation simple : la moyenne empirique tend vers l’espérance.

3.2 Exemple

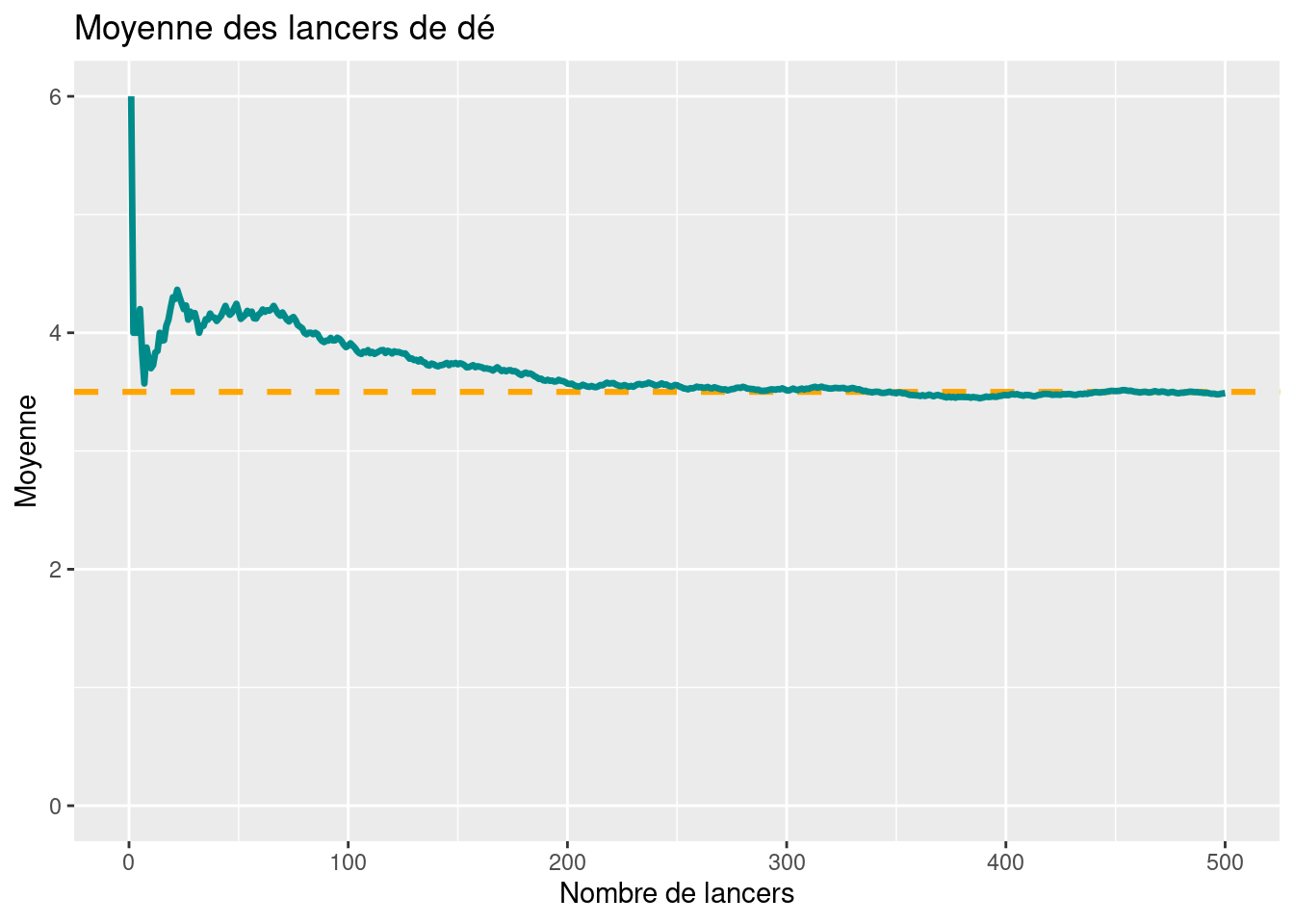
• Lançons un dé non truqué 500 fois et calculons la moyenne obtenue aprés chaque lancer
• Plus le nombre de lancers augmente, plus la moyenne converge vers \(3.5\)

library(ggplot2)

# Simuler les lancers de dés
set.seed(200)
n <- 500
ech <- sample(x = 1:6, size = n, replace = TRUE)
data <- data.frame(x = 1:n, 
                   p = sapply(1:n, 
                              function(i) mean(ech[1:i])))

# Tracer le graphique avec ggplot2
ggplot(data, aes(x = x, y = p)) +
  geom_hline(yintercept = 3.5, 
             color = "orange", 
             linetype = "dashed",
             linewidth = 1.1) +
  geom_line(color = "darkcyan", linewidth = 1.2) +
  labs(title = "Moyenne des lancers de dé",
       x = "Nombre de lancers",
       y = "Moyenne") +
  xlim(0, n) +
  ylim(0, 6)

4 Théorème Central Limite

4.1 Énoncé

Soit \((X_n)_{n\geq1}\) une suite de variables aléatoires iid avec une moyenne \(\mu\) et un écart-type \(\sigma\). Alors :

\[\lim_{n \to +\infty} \sqrt{n} \left( \frac{1}{n}\sum_{i=1}^{n} \frac{ X_i - \mu}{\sigma} \right) \xrightarrow{\mathcal {L}} N(0, 1)\]

Formulation simple : La différence entre moyenne empirique et espérance (\(\overline{X}_n - \mathbb{E}(X)\)) converge en loi vers une loi Normale

4.2 Exemple

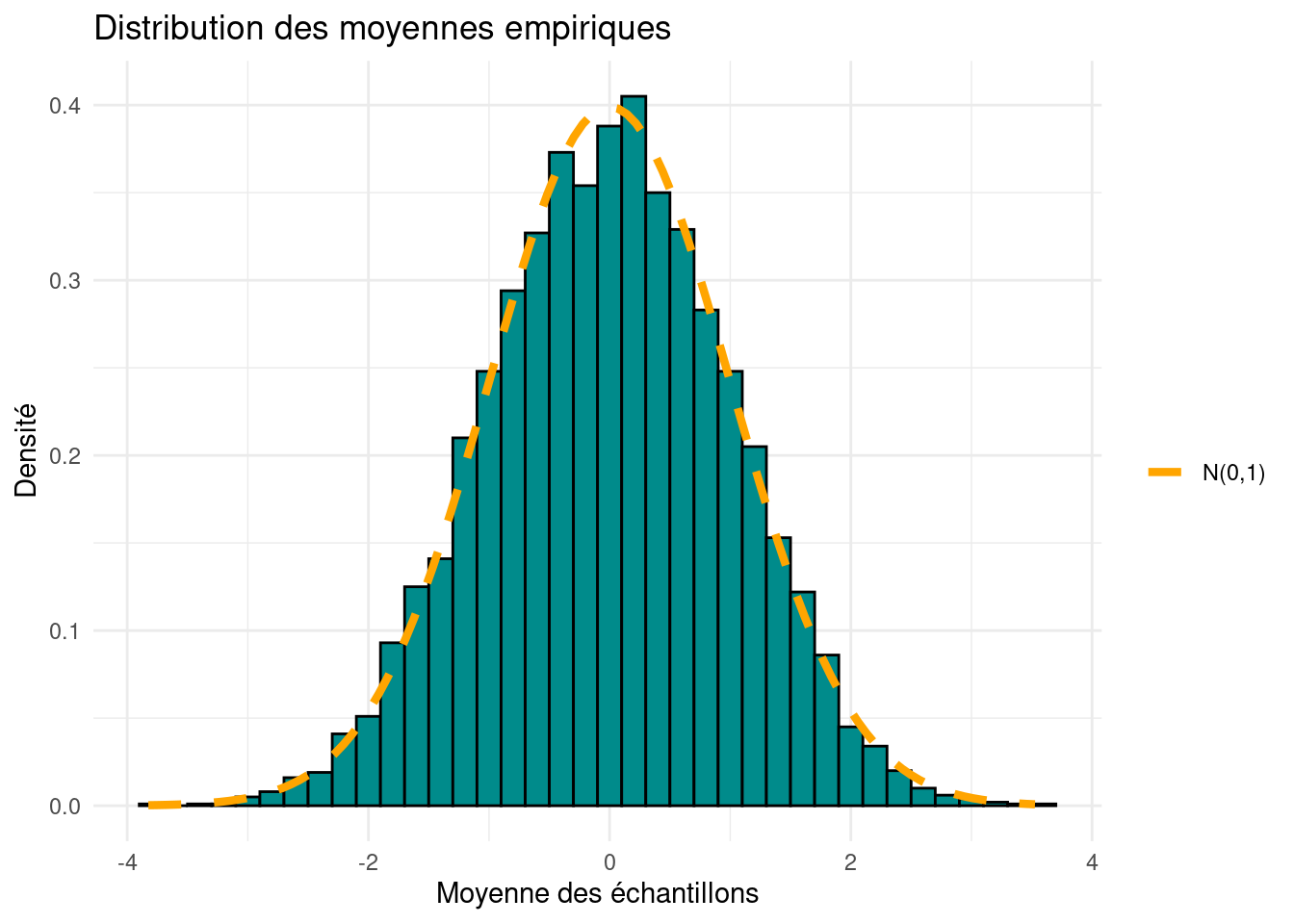
• Tirons un échantillon de 50 valeurs suivant la loi uniforme sur [0,1] et calculons la moyenne
• Répétons cette opération 5000 fois et affichons la distribution des moyennes empiriques obtenues

library(ggplot2)

# Paramètres
set.seed(200)
nb_sim <- 5000
taille_ech <- 50
u_min <- 0
u_max <- 1
E <- (u_max - u_min) / 2
V <- (u_max - u_min)^2 / 12

# Simulations
res <- numeric(nb_sim)
for (i in 1:nb_sim) {
  ech <- runif(taille_ech, min = u_min, max = u_max)
  res[i] <- sqrt(taille_ech) / sqrt(V) * (mean(ech) - E)
}

# Tracé de l'histogramme et de la densité
ggplot(data.frame(res), aes(x = res)) +
  geom_histogram(binwidth = 0.2, 
                 fill = "darkcyan", 
                 color = "black", 
                 aes(y = after_stat(density))) +
  stat_function(aes(linetype = "N(0,1)"), 
                fun = dnorm, 
                args = list(mean = 0, sd = 1), 
                color = "orange", 
                linewidth = 1.5) +
  labs(title = "Distribution des moyennes empiriques",
       x = "Moyenne des échantillons",
       y = "Densité") +
  scale_linetype_manual(name = "", 
                        values = "dashed",
                        labels = c("N(0,1)")) +
  theme_minimal()

4.3 Vidéo

StatQuest by Joshua Starmer