Analyse multivariée

Introduction aux méthodes factorielles (ACP, AFD, AFC, ACM)
Author

Ludovic Deneuville

Documentation et Sources

Les exemples utilisés sont repris du cours de Matthieu MARBAC dispensé à l’ENSAI en 2021.

Objectifs et Contexte

  • Vous disposez des données suivantes
    • \(n\) individus
    • \(p\) variables
    • \(X\) : matrice des données de dimension \(n\) x \(p\)
  • Comment analyser la structure et représenter ces données ?

Il n’ai pas aisé de représenter vos données en dimension \(p\) :

  • Nuage de points
    • représentation de vos données en dimension p
    • pour les calculs, le nuage de point sera centré et réduit
      • cela permet d’avoir le même poids pour chaque variable
      • par exemple en réduisant, une variable age (valeurs entre 0 et 120) aura la même importance qu’une variable nombre de neurones (valeurs entre 100 millions et 100 milliards)
      • ce n’est pas obligatoire de réduire, mais si on ne le fait pas, la variable age dont la variance est beaucoup plus faible, sera négligeable

🎯 Vous souhaitez par exemple représenter vos données sur un graphique en 2D.

Les méthodes factorielles sont là pour vous aider à réduire la complexité des données tout en préservant au maximum l’information qu’elles contiennent.

Comment ? En effectuant un changement de base pour obtenir des axes où l’inertie est maximale.

  • Inertie
    • représente l’écart entre les observations
    • grande si le nuage est dispersé, petite sinon
    • l’inertie totale est égale à la somme des inerties de chaque axe
Autrement dit
  • Vous partez d’un nuage de point de dimension \(\mathbb{R}^p\)
  • Vous effectuez un changement de base
  • Pour le choix du 1er axe factoriel, vous cherchez l’axe qui maximise l’inertie
  • Puis vous cherchez un 2e axe factoriel qui maximise l’inertie restante
  • etc. jusqu’au dernier axe (p)
  • Enfin, vous analysez les premiers axes, ceux qui concentrent la majorité de l’inertie

Dans le domaine de l’analyse des données multivariées, plusieurs techniques sont couramment utilisées pour explorer la structure sous-jacente des données et en extraire des informations significatives.

Quatre de ces techniques employées sont :

  • l’Analyse en Composantes Principales (ACP)
  • l’Analyse Factorielle Discriminante (AFD)
  • l’Analyse Factorielle des Correspondances (AFC)
  • l’Analyse des Correspondances Multiples (ACM)

1 Ma première ACP

Nous allons commencer par réaliser une ACP. Les autres méthodes suivent globalement le même principe avec quelques variantes.

Pour réaliser une ACP, nous ne gardons que des variables quantitatives.

Important

Nous nous baserons sur un cas simple où :

  • tous les individus ont le même poids, c’est à dire la même importance
  • toutes les variables ont le même poids (Métrique : Identité)

1.1 Données

Commençons par réinitialiser notre environnement et charger les librairies utiles

rm(list=ls())

library(ggplot2)
library(FactoMineR)         # install.packages("FactoMineR")
library(factoextra)         # install.packages("factoextra")

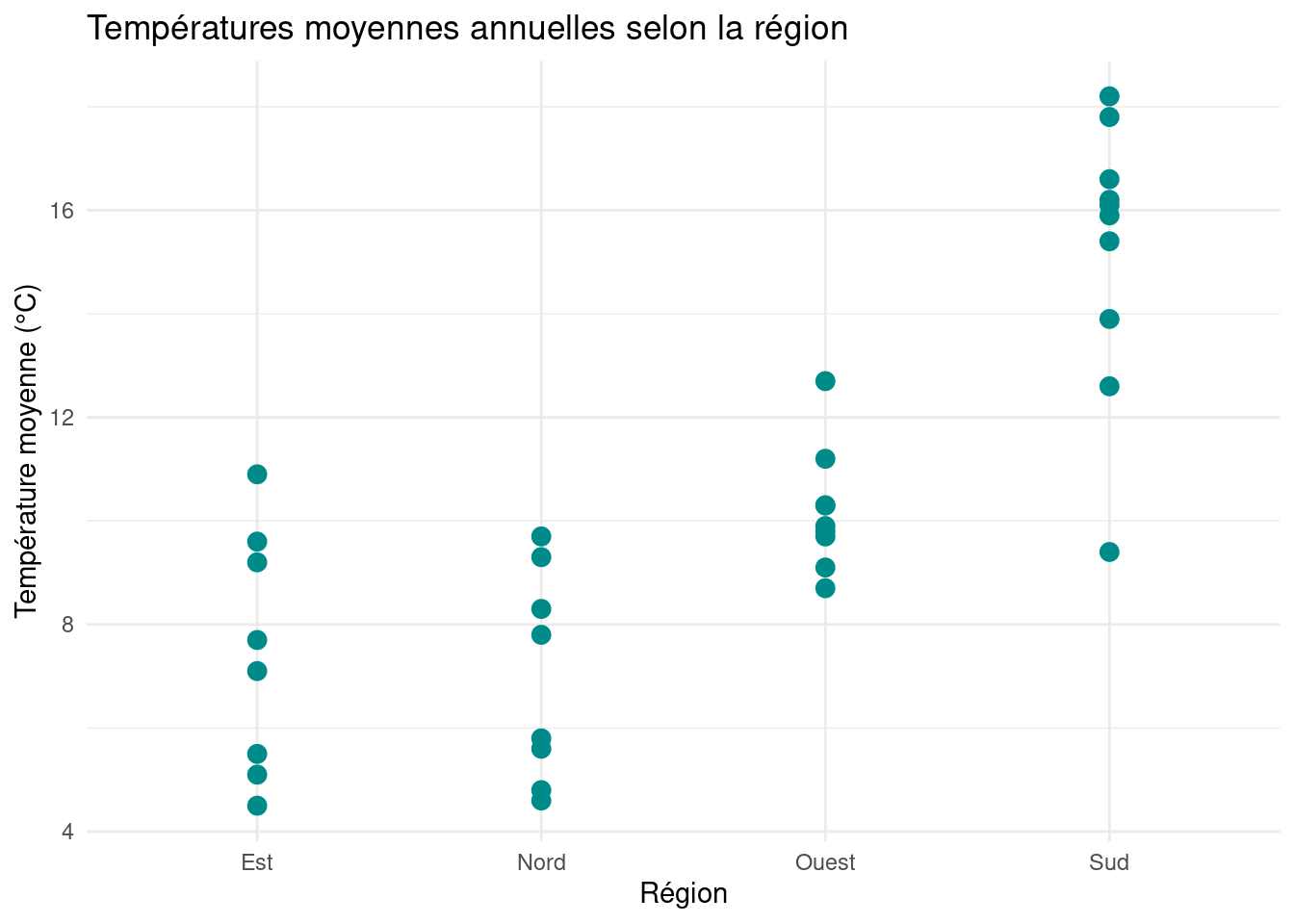
Nous utilisons un jeu de données contenant les températures de différentes villes d’Europe

temperature <- read.table("data/temperature.csv", 
                          header = TRUE,
                          sep = ";",
                          row.names = 1,
                          stringsAsFactors = TRUE)

str(temperature)
'data.frame':   35 obs. of  17 variables:
 $ Janvier  : num  2.9 9.1 -0.2 3.3 -1.1 -0.4 4.8 -5.8 -5.9 -3.7 ...
 $ Fevrier  : num  2.5 9.7 0.1 3.3 0.8 -0.4 5 -6.2 -5 -2 ...
 $ Mars     : num  5.7 11.7 4.4 6.7 5.5 1.3 5.9 -2.7 -0.3 1.9 ...
 $ Avril    : num  8.2 15.4 8.2 8.9 11.6 5.8 7.8 3.1 7.4 7.9 ...
 $ Mai      : num  12.5 20.1 13.8 12.8 17 11.1 10.4 10.2 14.3 13.2 ...
 $ Juin     : num  14.8 24.5 16 15.6 20.2 15.4 13.3 14 17.8 16.9 ...
 $ Juillet  : num  17.1 27.4 18.3 17.8 22 17.1 15 17.2 19.4 18.4 ...
 $ Aout     : num  17.1 27.2 18 17.8 21.3 16.6 14.6 14.9 18.5 17.6 ...
 $ Septembre: num  14.5 23.8 14.4 15 16.9 13.3 12.7 9.7 13.7 13.7 ...
 $ Octobre  : num  11.4 19.2 10 11.1 11.3 8.8 9.7 5.2 7.5 8.6 ...
 $ Novembre : num  7 14.6 4.2 6.7 5.1 4.1 6.7 0.1 1.2 2.6 ...
 $ Decembre : num  4.4 11 1.2 4.4 0.7 1.3 5.4 -2.3 -3.6 -1.7 ...
 $ Moyenne  : num  9.9 17.8 9.1 10.3 10.9 7.8 9.3 4.8 7.1 7.7 ...
 $ Amplitude: num  14.6 18.3 18.5 14.4 23.1 17.5 10.2 23.4 25.3 22.1 ...
 $ Latitude : num  52.2 37.6 52.3 50.5 47.3 55.4 53.2 60.1 50.3 50 ...
 $ Longitude: num  4.5 23.5 13.2 4.2 19 12.3 6.1 25 30.3 19.6 ...
 $ Region   : Factor w/ 4 levels "Est","Nord","Ouest",..: 3 4 3 3 1 2 2 2 1 1 ...

Pour chacune des villes, nous avons les variables suivantes :

  • 12 variables pour les températures moyennes pour chaque mois
  • la température moyenne de l’année, ainsi que l’amplitude
  • la latitude et la longitude
  • la région

Toutes les variables sont numériques, excepté la région.

1.2 Statistiques descriptives

Avant de se lancer tête baissée, regardons les statistiques descriptives

summary(temperature)
    Janvier          Fevrier            Mars            Avril       
 Min.   :-9.300   Min.   :-7.900   Min.   :-3.700   Min.   : 2.900  
 1st Qu.:-1.550   1st Qu.:-0.150   1st Qu.: 1.600   1st Qu.: 7.250  
 Median : 0.200   Median : 1.900   Median : 5.400   Median : 8.900  
 Mean   : 1.346   Mean   : 2.217   Mean   : 5.229   Mean   : 9.283  
 3rd Qu.: 4.900   3rd Qu.: 5.800   3rd Qu.: 8.500   3rd Qu.:12.050  
 Max.   :10.700   Max.   :11.800   Max.   :14.100   Max.   :16.900  
      Mai             Juin          Juillet           Aout      
 Min.   : 6.50   Min.   : 9.30   Min.   :11.10   Min.   :10.60  
 1st Qu.:12.15   1st Qu.:15.40   1st Qu.:17.30   1st Qu.:16.65  
 Median :13.80   Median :16.90   Median :18.90   Median :18.30  
 Mean   :13.91   Mean   :17.41   Mean   :19.62   Mean   :18.98  
 3rd Qu.:16.35   3rd Qu.:19.80   3rd Qu.:21.75   3rd Qu.:21.60  
 Max.   :20.90   Max.   :24.50   Max.   :27.40   Max.   :27.20  
   Septembre        Octobre         Novembre         Decembre    
 Min.   : 7.90   Min.   : 4.50   Min.   :-1.100   Min.   :-6.00  
 1st Qu.:13.00   1st Qu.: 8.65   1st Qu.: 3.200   1st Qu.: 0.25  
 Median :14.80   Median :10.20   Median : 5.100   Median : 1.70  
 Mean   :15.63   Mean   :11.00   Mean   : 6.066   Mean   : 2.88  
 3rd Qu.:18.25   3rd Qu.:13.30   3rd Qu.: 7.900   3rd Qu.: 5.40  
 Max.   :24.30   Max.   :19.40   Max.   :14.900   Max.   :12.00  
    Moyenne        Amplitude        Latitude       Longitude       Region  
 Min.   : 4.50   Min.   :10.20   Min.   :37.20   Min.   : 0.00   Est  : 8  
 1st Qu.: 7.75   1st Qu.:14.90   1st Qu.:43.90   1st Qu.: 4.35   Nord : 8  
 Median : 9.70   Median :18.50   Median :50.00   Median : 9.40   Ouest: 9  
 Mean   :10.27   Mean   :18.32   Mean   :48.77   Mean   :11.98   Sud  :10  
 3rd Qu.:12.65   3rd Qu.:21.45   3rd Qu.:52.75   3rd Qu.:18.65             
 Max.   :18.20   Max.   :27.60   Max.   :64.10   Max.   :30.30             
ggplot(temperature, aes(x = Region, y = Moyenne)) +
  geom_point(size = 3, color="darkcyan") +
  labs(title = "Températures moyennes annuelles selon la région",
       x = "Région",
       y = "Température moyenne (°C)") +
  theme_minimal()

1.3 Sélection des variables

La première étape consiste à sélectionner les variables et individus qui vont servir à réaliser l’ACP.

  • variables actives : variables qui serviront à calculer les nouveaux axes
  • individus actifs : individus qui serviront à calculer les nouveaux axes
  • individus et variables supplémentaires : individus et variables qui ne serviront pas à la création des nouveaux axes mais dont on souhaite observer la position sur ces nouveaux axes
    • ils peuvent servir pour contrôler la pertinence de la nouvelle base

Ces choix peuvent différer selon l’analyse que nous souhaitons réaliser. Ici nous choisissons par exemple :

  • variables actives : les températures de janvier à décembre
    • les colonnes 13 à 16 sont des variables quantitatives supplémentaires
    • la colonne 17 est une variable qualitative supplémentaire
  • individus actifs : les capitales
    • les autres (lignes 24 à 35) seront supplémentaires
res_acp <- PCA(temperature, 
               ind.sup = c(24:35),
               quanti.sup = c(13:16),
               quali.sup = c(17),
               graph = FALSE)

Voici les coordonnées des villes dans la nouvelle base :

res_acp$ind$coord
                 Dim.1        Dim.2       Dim.3        Dim.4        Dim.5
Amsterdam   0.22693852 -1.371378702 -0.10439354 -0.282792759 -0.225234980
Athenes     7.60067204  0.930375742  0.56142895 -0.286557237  0.121284086
Berlin     -0.28785832  0.016454075 -0.29060835 -0.055593051 -0.141777442
Bruxelles   0.63117358 -1.177217640 -0.15204276  0.017069866 -0.118080300
Budapest    1.66802839  1.712697730 -0.49898331  0.112436553  0.147493796
Copenhague -1.46239513 -0.492056307  0.44036858 -0.176716151  0.001359796
Dublin     -0.50524137 -2.673496925 -0.17850939  0.029911177  0.199489106
Helsinki   -4.03629712  0.462039367  0.59318909 -0.244444751  0.058755870
Kiev       -1.71222008  2.007597607 -0.17067034 -0.112807425  0.046761788
Cracovie   -1.25865727  0.874989077 -0.27396329  0.036537296 -0.022272155
Lisbonne    5.59928833 -1.554345838 -0.27035193 -0.137240393  0.057997452
Londres     0.05764006 -1.573766723 -0.08467398  0.052014838  0.166383037
Madrid      4.06406743  0.697664862  0.46179949  0.662933274 -0.076738822
Minsk      -3.23789748  1.391289730 -0.07227015 -0.183341936  0.066896667
Moscou     -3.46261171  2.182015808 -0.30130242 -0.005382798  0.075779200
Oslo       -3.30598698  0.310053024  0.29530945  0.190608834  0.068558517
Paris       1.41971350 -0.897598545 -0.11032749 -0.079067225 -0.184884193
Prague     -0.10900287  0.698041163 -0.24257136  0.100375201  0.119810451
Reykjavik  -4.70406435 -2.957197699 -0.05789842  0.195366437  0.102746920
Rome        5.38200124  0.293698723  0.18926869 -0.012589110  0.077649640
Sarajevo    0.16345193  0.319489453 -0.36458614  0.073615022 -0.204664346
Sofia       0.41781097  0.795074460 -0.24086374  0.047803563 -0.195020427
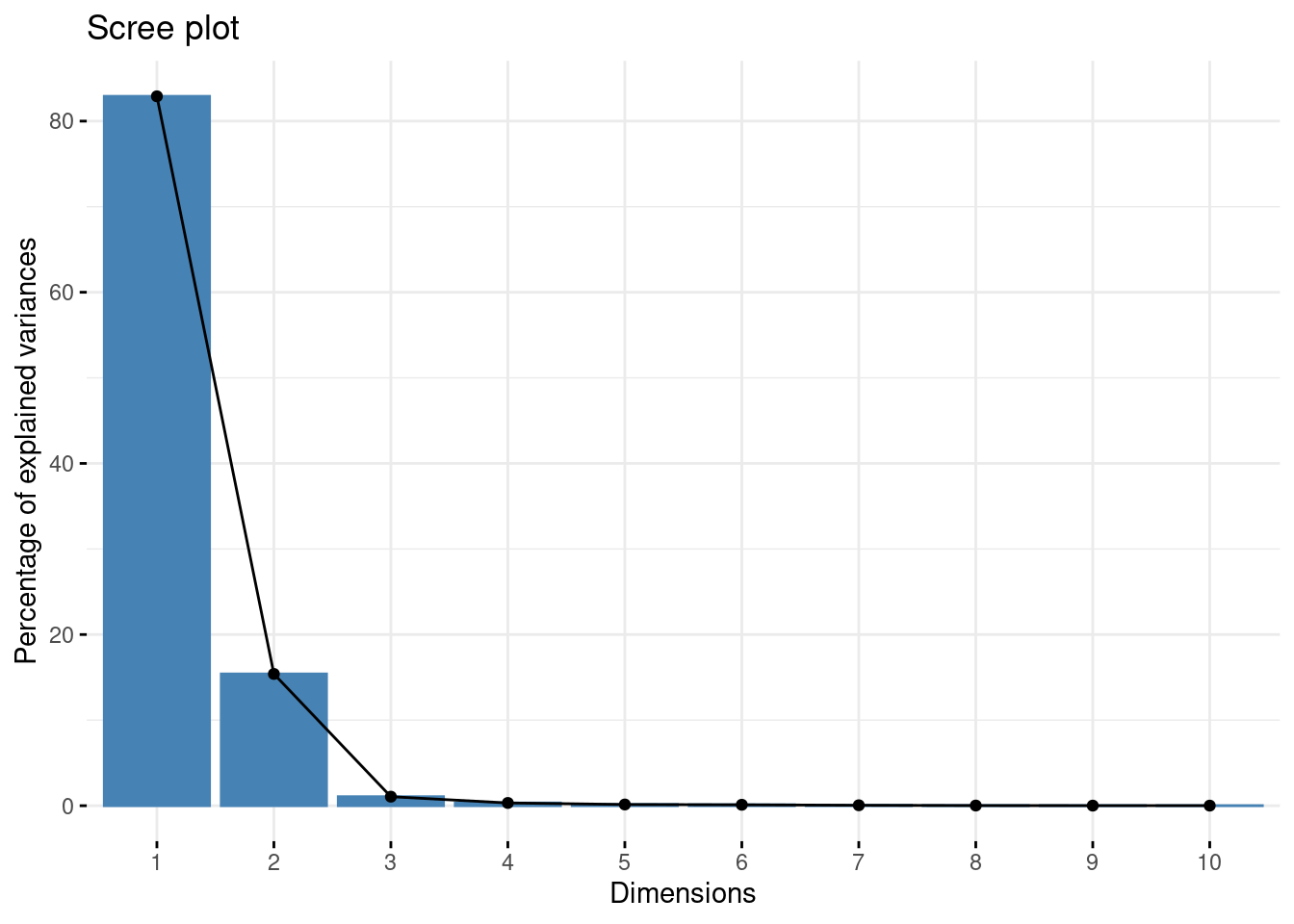
Stockholm  -3.14855331  0.005577557  0.87265235  0.057860775 -0.142293659

1.4 Inertie par axe

La dimension 1 est l’axe avec la plus grande inertie, la dimension 2 avec la 2e plus grande inertie…

fviz_eig(res_acp)

Le premier axe explique 82.9 % de l’inertie et le second 15,4 %.

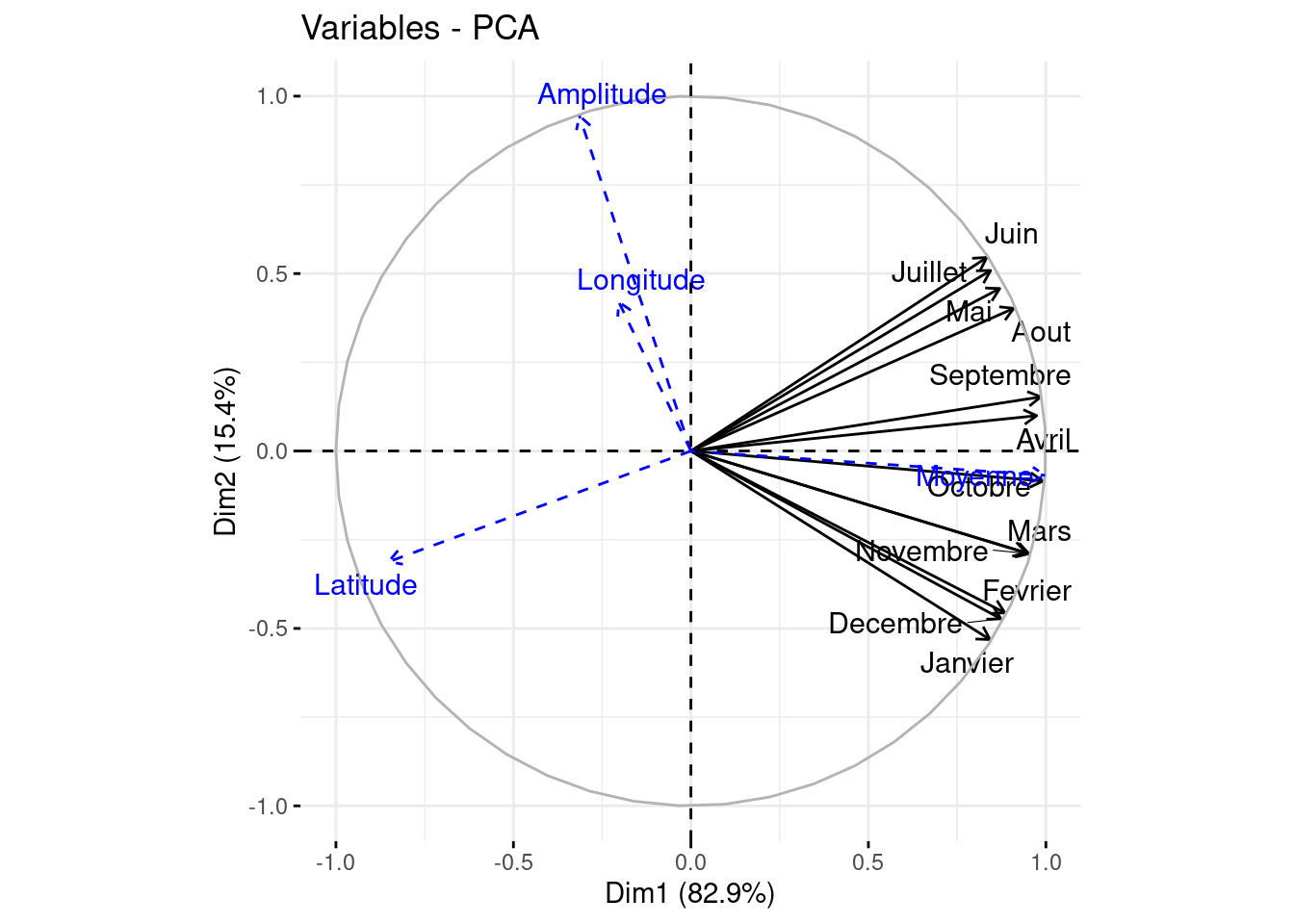
1.5 Cercle des corrélations

Le cercle des corrélations permet de représenter graphiquement les corrélations entre les variables et les axes factoriels.

Représentons ce cercle pour les 2 premiers axes :

fviz_pca_var(res_acp, repel = TRUE)

  • Interprétations des flèches. Si elle pointe prés de
    • [1,0], la variable est fortement corrélée positivement à l’axe factoriel des abscisses (1)
    • [-1,0], la variable est fortement corrélée négativement à l’axe factoriel des abscisses (1)
    • [0,1], la variable est fortement corrélée positivement à l’axe factoriel des ordonnées (2)
    • [0,-1], la variable est fortement corrélée négativement à l’axe factoriel des ordonnées (2)
    • [0,0], la variable n’est corrélé à aucun axe factoriel

Dans notre exemple, les 12 variables de températures moyennes mensuelle sont fortement correlés positivement à l’axe 1. Ce comportement est nommé effet taille.

C’est assez logique car cet axe représente une écrasante majorité de l’inertie.

Autre information interessante : la variable Amplitude est fortement correlée au 2e axe. Et pour tant cette variable est supplémentaire et n’a donc pas été prise en compte pour construire cet axe.

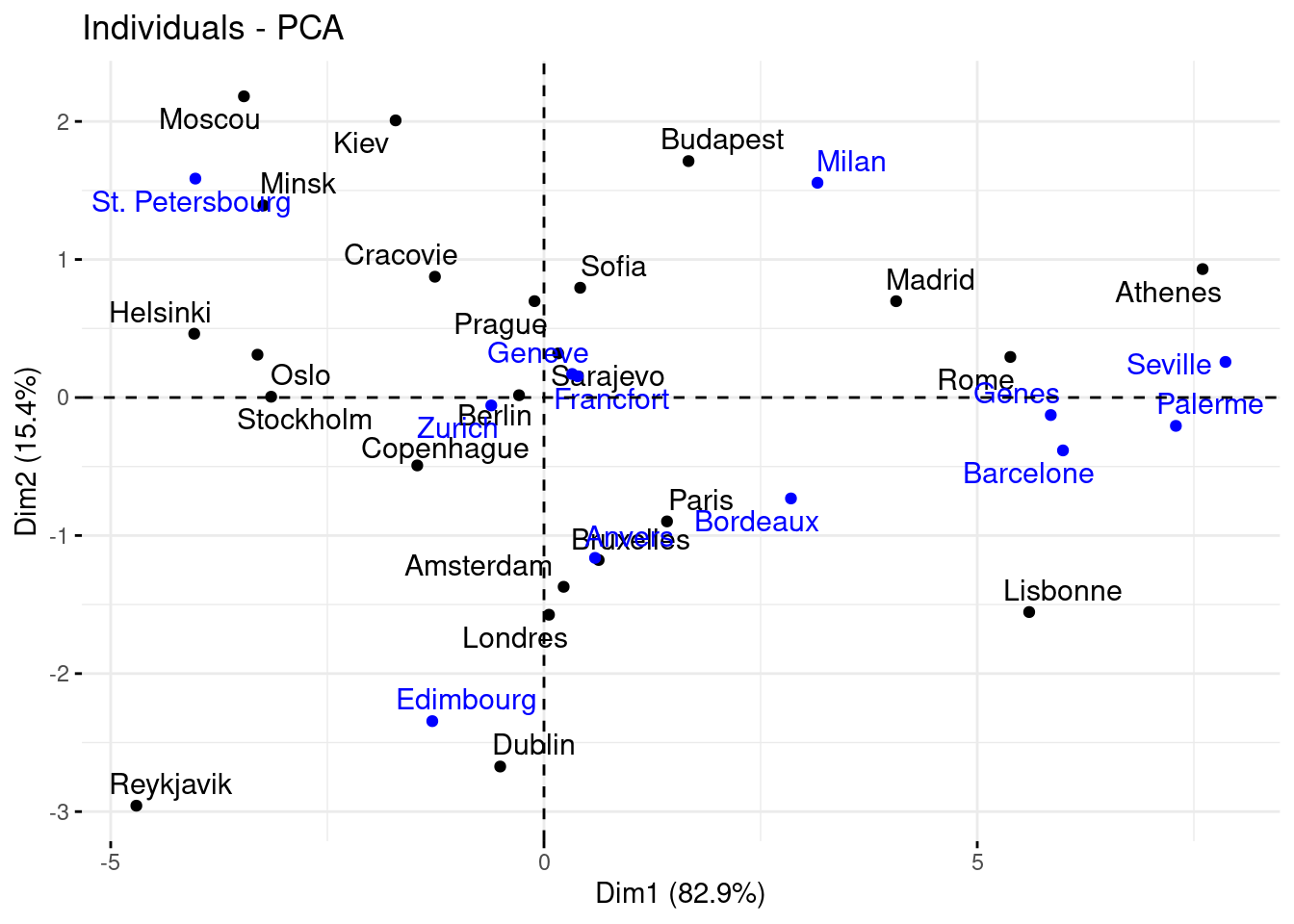
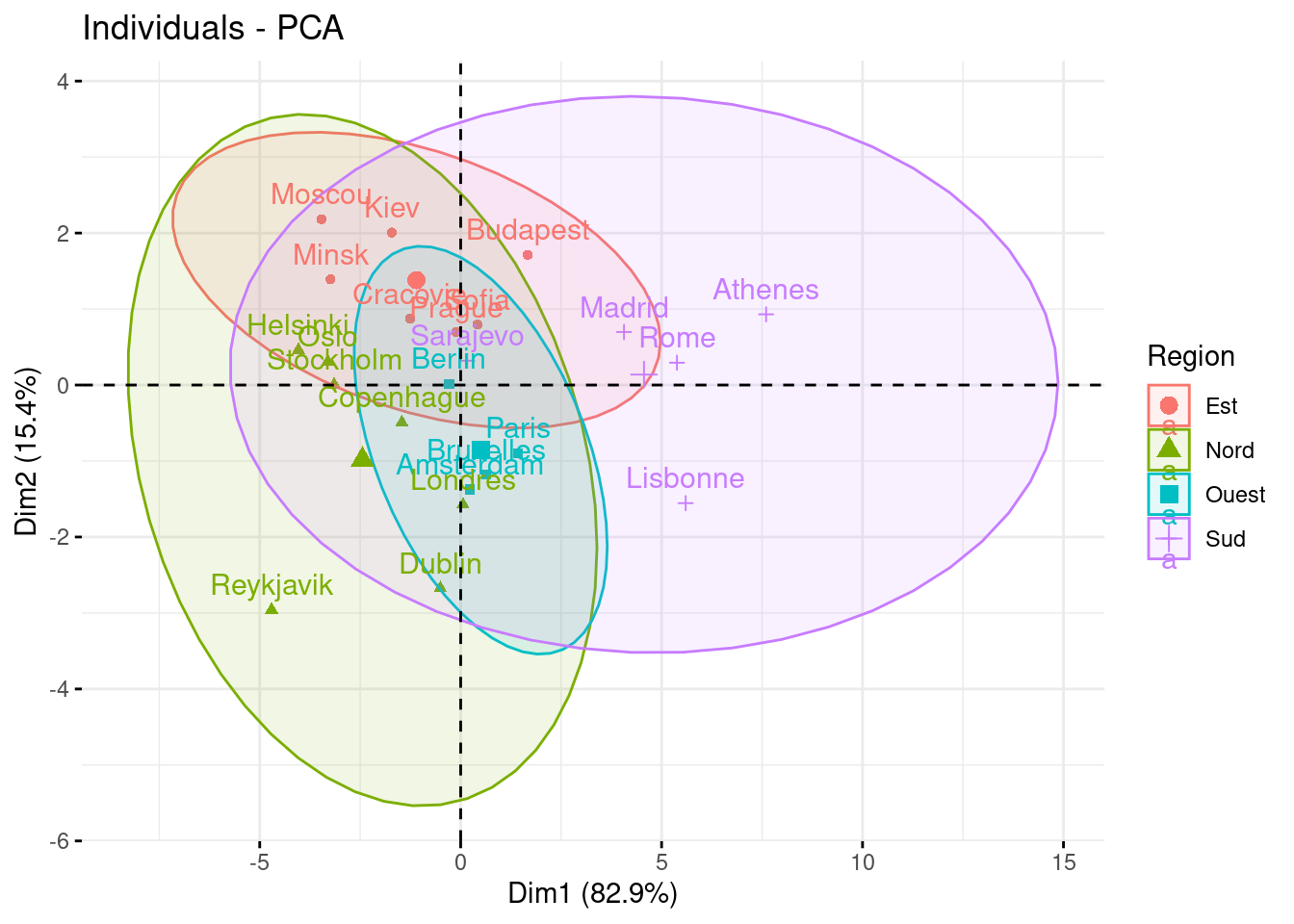
1.6 Individus sur les 2 premiers axes

Représentons maintenant les individus sur les axes factoriels.

fviz_pca_ind(res_acp, repel = TRUE)

Essayons d’interpréter ces 2 axes :

  • axe 1 : nous retrouvons des villes où les températures sont plutôt froides à gauche et chaudes à droite
  • axe 2 :
    • en haut nous retrouvons des villes avec un climat continental (grandes variations de températures entre les saisons)
    • alors qu’en bas, nous retrouvons plutôt des villes avec un climat océanique (températures plus stables)
fviz_pca_ind(res_acp,
             habillage = "Region", 
             addEllipses = TRUE,
             invisible = c("ind.sup"))

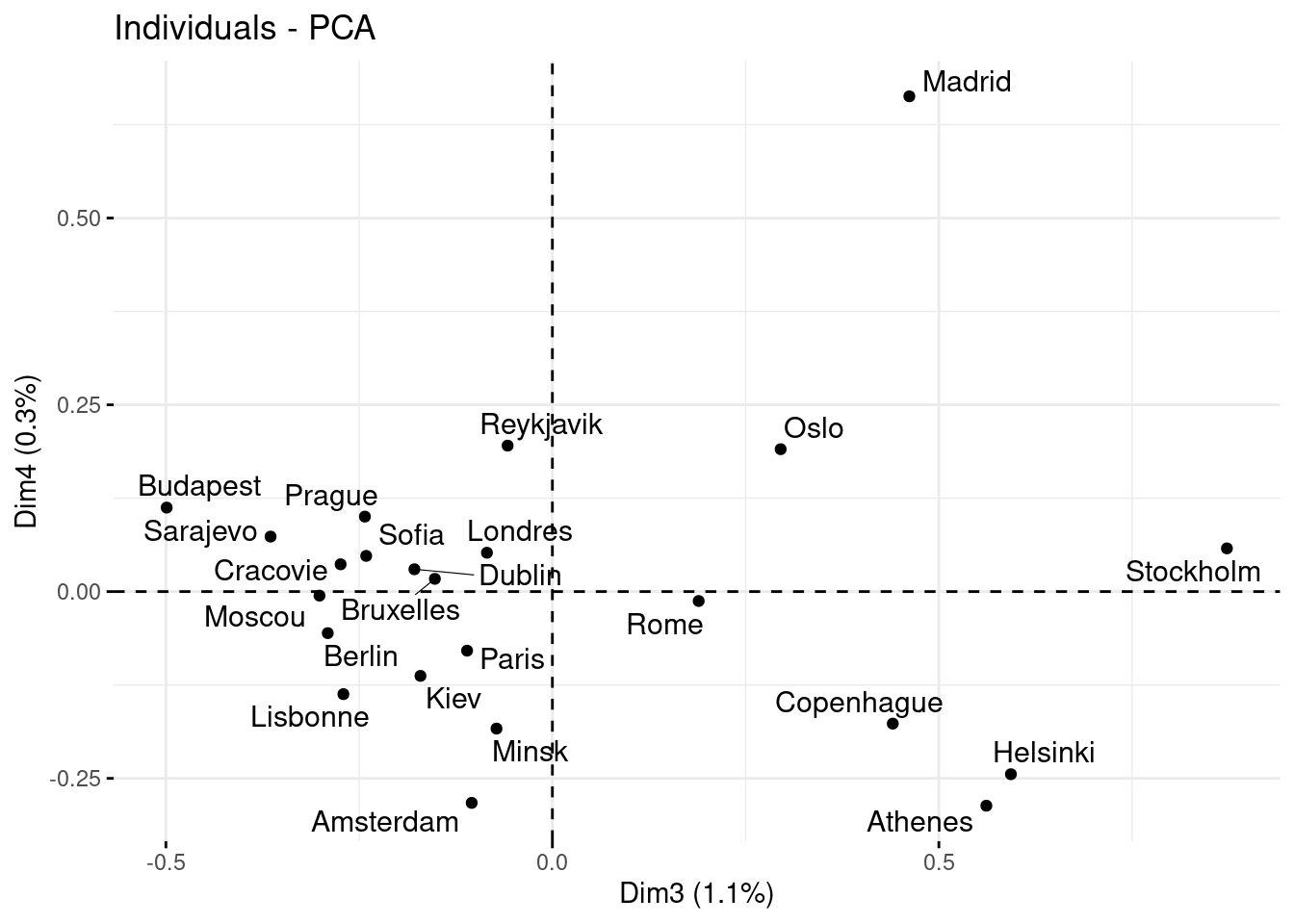
Nous pouvons également visualiser les individus sur les autres axes.

Dans le cas présent l’inertie des axes 3 et 4 est très faible, il est donc compliqué d’interpréter ces axes.

fviz_pca_ind(res_acp,
             repel = TRUE,
             axes = c(3,4),
             invisible = c("ind.sup"))

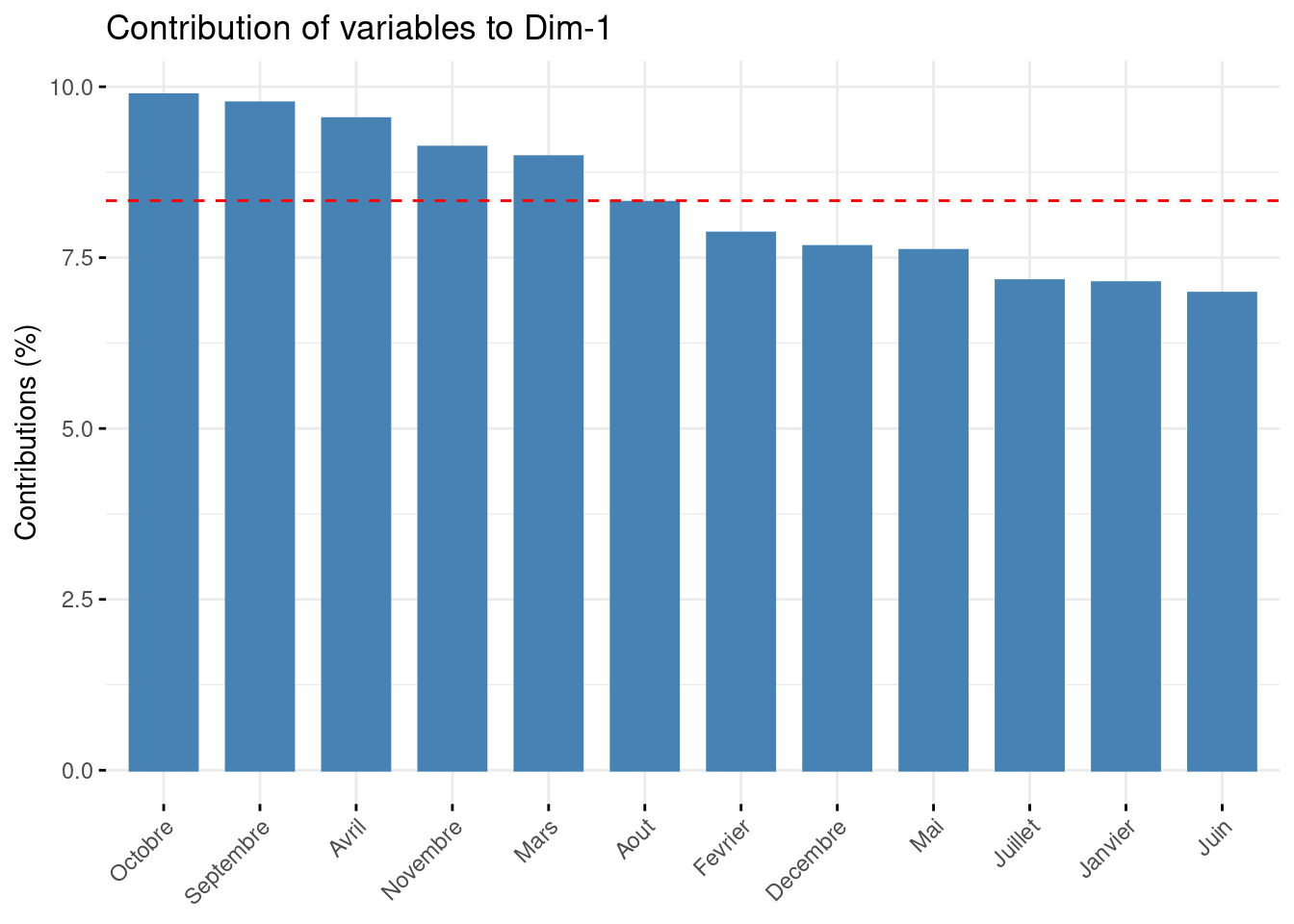
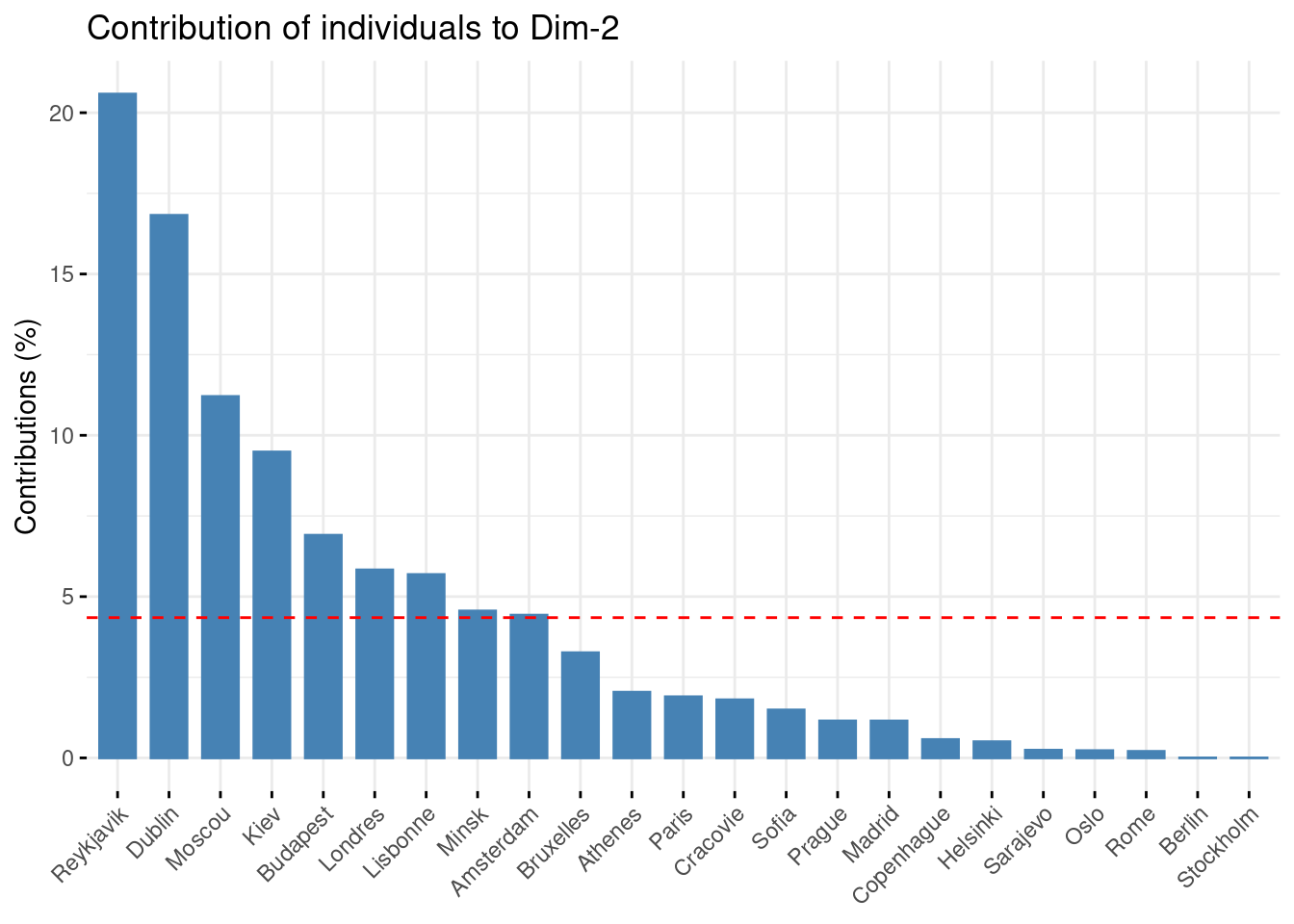
1.7 Contribution aux axes

La contribution aux axes d’une variable indique si la variable a fortement contribué pour la construction de cet axe.

  • plus une variable contribue à une composante principale, plus sa contribution aux axes sera élevée
  • cette mesure permet d’identifier les variables qui ont le plus d’impact sur chaque composante principale
fviz_contrib(res_acp, choice = "var", axes = 1)

Il en va de même pour la contribution aux axes d’un individu.

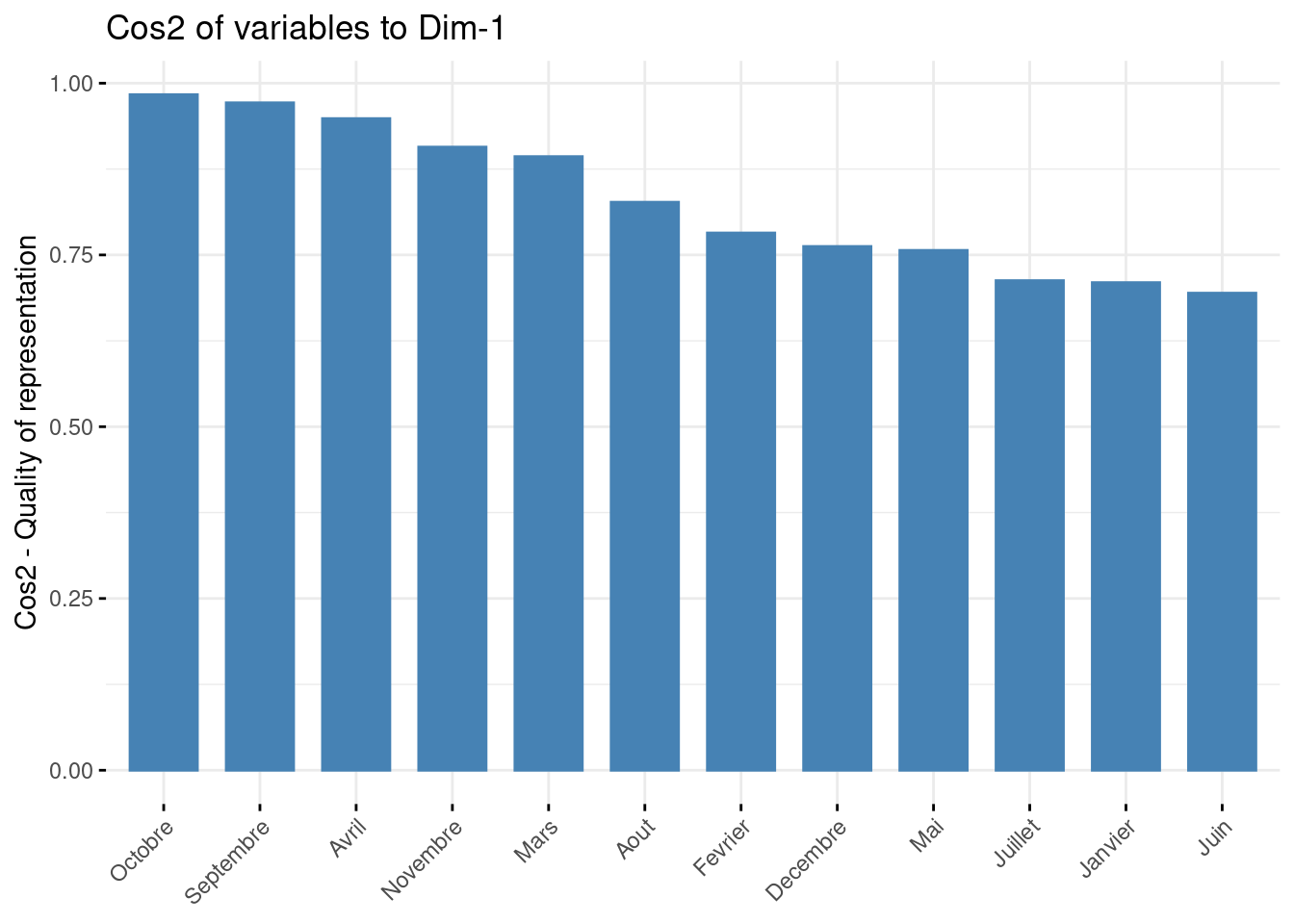
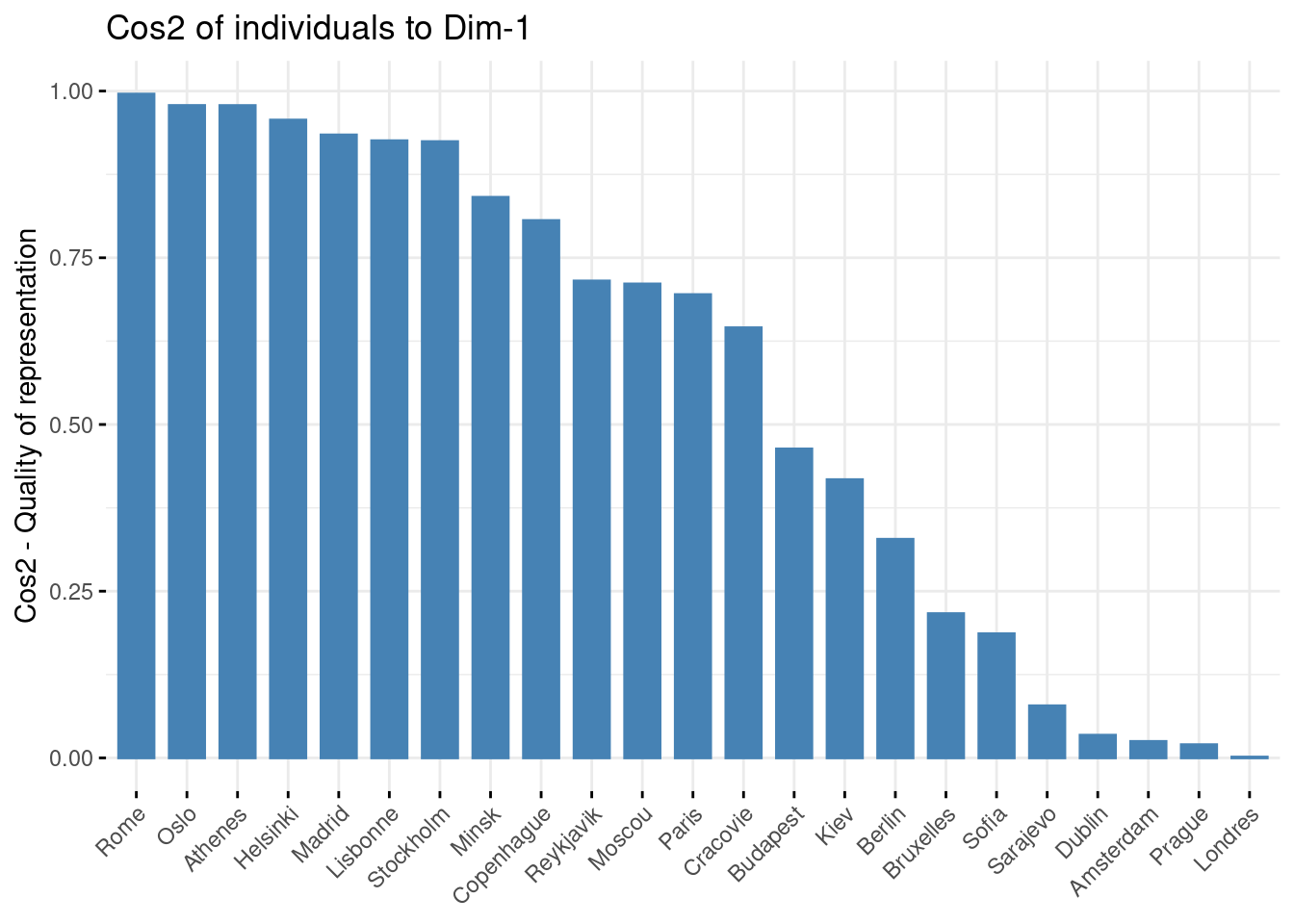
fviz_contrib(res_acp, choice = "ind", axes = 2)

1.8 Cos²

Le cos² mesure la qualité de représentation de chaque variable sur chaque axe.

  • un cos² proche de 1 indique une bonne représentation de la variable sur l’axe, ce qui signifie que la variable est bien alignée avec l’axe et contribue fortement à sa définition
  • un cos² proche de 0 indique une faible représentation de la variable sur l’axe, ce qui signifie que la variable n’est pas bien alignée avec l’axe et contribue peu à sa définition
fviz_cos2(res_acp, choice = "var", axe = 1)

Idem pour les individus.

fviz_cos2(res_acp, choice = "ind", axe = 1)

2 Vision mathématique

2.1 Matrices des données

X <- as.matrix(temperature[1:23,1:12])
colnames(X) <- c("jan", "fev", "mar", "avr", "mai", "jui", "jul", "aou", "sep", "oct", "nov", "dec")

X
            jan  fev  mar  avr  mai  jui  jul  aou  sep  oct  nov  dec
Amsterdam   2.9  2.5  5.7  8.2 12.5 14.8 17.1 17.1 14.5 11.4  7.0  4.4
Athenes     9.1  9.7 11.7 15.4 20.1 24.5 27.4 27.2 23.8 19.2 14.6 11.0
Berlin     -0.2  0.1  4.4  8.2 13.8 16.0 18.3 18.0 14.4 10.0  4.2  1.2
Bruxelles   3.3  3.3  6.7  8.9 12.8 15.6 17.8 17.8 15.0 11.1  6.7  4.4
Budapest   -1.1  0.8  5.5 11.6 17.0 20.2 22.0 21.3 16.9 11.3  5.1  0.7
Copenhague -0.4 -0.4  1.3  5.8 11.1 15.4 17.1 16.6 13.3  8.8  4.1  1.3
Dublin      4.8  5.0  5.9  7.8 10.4 13.3 15.0 14.6 12.7  9.7  6.7  5.4
Helsinki   -5.8 -6.2 -2.7  3.1 10.2 14.0 17.2 14.9  9.7  5.2  0.1 -2.3
Kiev       -5.9 -5.0 -0.3  7.4 14.3 17.8 19.4 18.5 13.7  7.5  1.2 -3.6
Cracovie   -3.7 -2.0  1.9  7.9 13.2 16.9 18.4 17.6 13.7  8.6  2.6 -1.7
Lisbonne   10.5 11.3 12.8 14.5 16.7 19.4 21.5 21.9 20.4 17.4 13.7 11.1
Londres     3.4  4.2  5.5  8.3 11.9 15.1 16.9 16.5 14.0 10.2  6.3  4.4
Madrid      5.0  6.6  9.4 12.2 16.0 20.8 24.7 24.3 19.8 13.9  8.7  5.4
Minsk      -6.9 -6.2 -1.9  5.4 12.4 15.9 17.4 16.3 11.6  5.8  0.1 -4.2
Moscou     -9.3 -7.6 -2.0  6.0 13.0 16.6 18.3 16.7 11.2  5.1 -1.1 -6.0
Oslo       -4.3 -3.8 -0.6  4.4 10.3 14.9 16.9 15.4 11.1  5.7  0.5 -2.9
Paris       3.7  3.7  7.3  9.7 13.7 16.5 19.0 18.7 16.1 12.5  7.3  5.2
Prague     -1.3  0.2  3.6  8.8 14.3 17.6 19.3 18.7 14.9  9.4  3.8  0.3
Reykjavik  -0.3  0.1  0.8  2.9  6.5  9.3 11.1 10.6  7.9  4.5  1.7  0.2
Rome        7.1  8.2 10.5 13.7 17.8 21.7 24.4 24.1 20.9 16.5 11.7  8.3
Sarajevo   -1.4  0.8  4.9  9.3 13.8 17.0 18.9 18.7 15.2 10.5  5.1  0.8
Sofia      -1.7  0.2  4.3  9.7 14.3 17.7 20.0 19.5 15.8 10.7  5.0  0.6
Stockholm  -3.5 -3.5 -1.3  3.5  9.2 14.6 17.2 16.0 11.7  6.5  1.7 -1.6

2.2 Matrice des variances-covariances

C’est une matrice carrée symétrique qui contient :

  • les variances des variables sur la diagonale
  • les covariances entre les paires de variables hors-diagonale
matrice_var_cov <- cov(X); 

round(matrice_var_cov, 1)
     jan  fev  mar  avr  mai  jui  jul  aou  sep  oct  nov  dec
jan 26.8 26.2 21.9 13.6  7.5  6.8  8.0 10.4 14.6 18.0 21.0 23.7
fev 26.2 26.2 22.3 14.6  8.6  7.9  9.0 11.5 15.5 18.4 21.0 23.2
mar 21.9 22.3 20.2 14.3  9.6  8.8  9.8 12.0 15.0 17.0 18.5 19.6
avr 13.6 14.6 14.3 12.1  9.7  9.3 10.0 11.4 12.7 13.1 13.1 12.6
mai  7.5  8.6  9.6  9.7  9.2  9.2  9.7 10.4 10.5  9.9  8.9  7.5
jui  6.8  7.9  8.8  9.3  9.2  9.9 10.5 11.1 10.7  9.7  8.5  6.9
jul  8.0  9.0  9.8 10.0  9.7 10.5 11.6 12.1 11.7 10.6  9.5  8.0
aou 10.4 11.5 12.0 11.4 10.4 11.1 12.1 13.0 13.0 12.4 11.4 10.1
sep 14.6 15.5 15.0 12.7 10.5 10.7 11.7 13.0 14.2 14.4 14.3 13.7
oct 18.0 18.4 17.0 13.1  9.9  9.7 10.6 12.4 14.4 15.7 16.3 16.6
nov 21.0 21.0 18.5 13.1  8.9  8.5  9.5 11.4 14.3 16.3 17.9 19.1
dec 23.7 23.2 19.6 12.6  7.5  6.9  8.0 10.1 13.7 16.6 19.1 21.3
# On centre toutes les variables
centered_X <- scale(X, center = TRUE, scale = FALSE)

round(1/(nrow(centered_X)-1) * t(centered_X) %*% centered_X, 1)
     jan  fev  mar  avr  mai  jui  jul  aou  sep  oct  nov  dec
jan 26.8 26.2 21.9 13.6  7.5  6.8  8.0 10.4 14.6 18.0 21.0 23.7
fev 26.2 26.2 22.3 14.6  8.6  7.9  9.0 11.5 15.5 18.4 21.0 23.2
mar 21.9 22.3 20.2 14.3  9.6  8.8  9.8 12.0 15.0 17.0 18.5 19.6
avr 13.6 14.6 14.3 12.1  9.7  9.3 10.0 11.4 12.7 13.1 13.1 12.6
mai  7.5  8.6  9.6  9.7  9.2  9.2  9.7 10.4 10.5  9.9  8.9  7.5
jui  6.8  7.9  8.8  9.3  9.2  9.9 10.5 11.1 10.7  9.7  8.5  6.9
jul  8.0  9.0  9.8 10.0  9.7 10.5 11.6 12.1 11.7 10.6  9.5  8.0
aou 10.4 11.5 12.0 11.4 10.4 11.1 12.1 13.0 13.0 12.4 11.4 10.1
sep 14.6 15.5 15.0 12.7 10.5 10.7 11.7 13.0 14.2 14.4 14.3 13.7
oct 18.0 18.4 17.0 13.1  9.9  9.7 10.6 12.4 14.4 15.7 16.3 16.6
nov 21.0 21.0 18.5 13.1  8.9  8.5  9.5 11.4 14.3 16.3 17.9 19.1
dec 23.7 23.2 19.6 12.6  7.5  6.9  8.0 10.1 13.7 16.6 19.1 21.3

2.3 Matrice de corrélation

C’est la matrice des variances-covariances normalisée.

matrice_cor <- cor(X); 

round(matrice_cor, 2)
     jan  fev  mar  avr  mai  jui  jul  aou  sep  oct  nov  dec
jan 1.00 0.99 0.94 0.75 0.48 0.42 0.45 0.56 0.75 0.88 0.96 0.99
fev 0.99 1.00 0.97 0.82 0.56 0.49 0.52 0.62 0.80 0.91 0.97 0.98
mar 0.94 0.97 1.00 0.92 0.70 0.62 0.64 0.74 0.89 0.96 0.97 0.95
avr 0.75 0.82 0.92 1.00 0.92 0.86 0.84 0.91 0.97 0.95 0.89 0.78
mai 0.48 0.56 0.70 0.92 1.00 0.97 0.94 0.96 0.92 0.83 0.69 0.54
jui 0.42 0.49 0.62 0.86 0.97 1.00 0.99 0.98 0.90 0.78 0.64 0.47
jul 0.45 0.52 0.64 0.84 0.94 0.99 1.00 0.99 0.91 0.79 0.66 0.51
aou 0.56 0.62 0.74 0.91 0.96 0.98 0.99 1.00 0.96 0.87 0.75 0.61
sep 0.75 0.80 0.89 0.97 0.92 0.90 0.91 0.96 1.00 0.97 0.90 0.79
oct 0.88 0.91 0.96 0.95 0.83 0.78 0.79 0.87 0.97 1.00 0.97 0.91
nov 0.96 0.97 0.97 0.89 0.69 0.64 0.66 0.75 0.90 0.97 1.00 0.98
dec 0.99 0.98 0.95 0.78 0.54 0.47 0.51 0.61 0.79 0.91 0.98 1.00
# On centre et réduit toutes les variables
normalized_X <- scale(X, center = TRUE, scale = TRUE)

round(1/(nrow(normalized_X)-1) * t(normalized_X) %*% normalized_X, 2)
     jan  fev  mar  avr  mai  jui  jul  aou  sep  oct  nov  dec
jan 1.00 0.99 0.94 0.75 0.48 0.42 0.45 0.56 0.75 0.88 0.96 0.99
fev 0.99 1.00 0.97 0.82 0.56 0.49 0.52 0.62 0.80 0.91 0.97 0.98
mar 0.94 0.97 1.00 0.92 0.70 0.62 0.64 0.74 0.89 0.96 0.97 0.95
avr 0.75 0.82 0.92 1.00 0.92 0.86 0.84 0.91 0.97 0.95 0.89 0.78
mai 0.48 0.56 0.70 0.92 1.00 0.97 0.94 0.96 0.92 0.83 0.69 0.54
jui 0.42 0.49 0.62 0.86 0.97 1.00 0.99 0.98 0.90 0.78 0.64 0.47
jul 0.45 0.52 0.64 0.84 0.94 0.99 1.00 0.99 0.91 0.79 0.66 0.51
aou 0.56 0.62 0.74 0.91 0.96 0.98 0.99 1.00 0.96 0.87 0.75 0.61
sep 0.75 0.80 0.89 0.97 0.92 0.90 0.91 0.96 1.00 0.97 0.90 0.79
oct 0.88 0.91 0.96 0.95 0.83 0.78 0.79 0.87 0.97 1.00 0.97 0.91
nov 0.96 0.97 0.97 0.89 0.69 0.64 0.66 0.75 0.90 0.97 1.00 0.98
dec 0.99 0.98 0.95 0.78 0.54 0.47 0.51 0.61 0.79 0.91 0.98 1.00

Comparaison avec les valeurs propres données par la fonction pca

data.frame(
  "PCA" = as.vector(res_acp$eig[,"eigenvalue"]),
  "à la main" = eigen(cor(X))$values
)
PCA à.la.main
9.9477504 9.9477504
1.8476485 1.8476485
0.1262558 0.1262558
0.0382934 0.0382934
0.0167094 0.0167094
0.0128330 0.0128330
0.0058303 0.0058303
0.0020319 0.0020319
0.0010235 0.0010235
0.0009528 0.0009528
0.0005368 0.0005368
0.0001342 0.0001342

L’inertie du premier axe est égale à :

\[\frac{Valeur\ propre\ 1}{Somme\ des\ valeurs\ propres}\]

eigen(cor(X))$values[1] / sum(eigen(cor(X))$values)
[1] 0.8289792

3 AFD

🚧

Une Analyse Factorielle Discriminante (AFD) est une ACP à laquelle nous ajoutons une variable qualitative.

4 AFC

🚧

Une Analyse Factorielle des Correspondances (AFC) eprmet d’étudier la liaison entre 2 variables qualitatives.

5 ACM

🚧

Une Analyse factorielle des correspondances multiples (ACM) généralise l’AFC en étudiant les liaisons entre plusieurs variables qualitatives.

6 Vidéos

StatQuest: ACP, idées principales :